早教吧作业答案频道 -->数学-->
如图,正方形AOCB的边长为4,反比例函数y=kx(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE.(1)求k的值;(2)反比例函数图象与线段BC交于点D,直线y=12x+b过点D与线段AB交于点F,延长OF
题目详情
如图,正方形AOCB的边长为4,反比例函数y=
(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE.
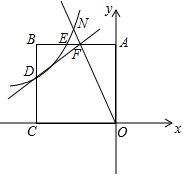
(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y=
x+b过点D与线段AB交于点F,延长OF交反比例函数y=
(x<0)的图象于点N,求N点坐标.
| k |
| x |

(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y=
| 1 |
| 2 |
| k |
| x |
▼优质解答
答案和解析
(1)∵S△AOE=3S△OBE,
∴AE=3BE,
∴AE=3,
∴E(-3,4)
反比例函数y=
(k≠0,且k为常数)的图象过点E,
∴4=
,即k=-12.
(2)∵正方形AOCB的边长为4,
∴点D的横坐标为-4,点F的纵坐标为4.
∵点D在反比例函数的图象上,
∴点D的纵坐标为3,即D(-4,3).
∵点D在直线y=
x+b上,
∴3=
×(-4)+b,解得b=5.
∴直线DF为y=
x+5,
将y=4代入y=
x+5,得4=
x+5,解得x=-2.
∴点F的坐标为(-2,4),
设直线OF的解析式为y=mx,
代入F的坐标得,4=-2m,
解得m=-2,
∴直线OF的解析式为y=-2x,
解
,得
.
∴N(-
,2
).
∴AE=3BE,
∴AE=3,
∴E(-3,4)
反比例函数y=
| k |
| x |
∴4=
| k |
| -3 |
(2)∵正方形AOCB的边长为4,
∴点D的横坐标为-4,点F的纵坐标为4.
∵点D在反比例函数的图象上,
∴点D的纵坐标为3,即D(-4,3).
∵点D在直线y=
| 1 |
| 2 |
∴3=
| 1 |
| 2 |
∴直线DF为y=
| 1 |
| 2 |
将y=4代入y=
| 1 |
| 2 |
| 1 |
| 2 |
∴点F的坐标为(-2,4),
设直线OF的解析式为y=mx,
代入F的坐标得,4=-2m,
解得m=-2,
∴直线OF的解析式为y=-2x,
解
|
|
∴N(-
| 6 |
| 6 |
看了 如图,正方形AOCB的边长为...的网友还看了以下:
求下列函数的最大值和最小值送分~f(x)=6x2+x+2x属于[-1,1]f(x)=6-12X+X 2020-04-26 …
(2014•苏州)如图,已知函数y=-12x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的 2020-06-08 …
(2014•日照二模)已知:如图,一次函数y=12x+1的图象与x轴交于点A,与y轴交于点B;二次 2020-06-14 …
如图,在矩形OABC中,点A、C的坐标分别为(10,0),(0,2),点D是线段BC上的动点(与端 2020-06-19 …
(2014•自贡)如图,已知抛物线y=ax2-32x+c与x轴相交于A、B两点,并与直线y=12x 2020-07-10 …
如图,已知函数y=-12x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M 2020-08-01 …
如图,在平面直角坐标系中,抛物线y=-x2+bx经过A(2,0),直线y=12x+m分别交x轴、y 2020-08-01 …
若4X—5Y=0,且Y不等于0,求12X+5Y分之12x—5Y的值. 2020-10-31 …
如果4x-5y=0,且x不等于0,那么12x-5y除以12x+5y的值是多少? 2020-10-31 …
如图,函数y=-2x+3与y=-12x+m的图象交于P(n,-2).(1)求出m、n的值;(2)直接 2020-11-01 …