早教吧作业答案频道 -->数学-->
已知四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥平面ABCD,PA=AB=AC=2,AD=22,点E是线段AB上靠近B点的三等分点,点F、G分别在线段PD、PC上.(Ⅰ)证明:CD⊥AG;(Ⅱ)若三棱锥E-BCF的体积为16,
题目详情
已知四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥平面ABCD,PA=AB=AC=2,AD=2
,点E是线段AB上靠近B点的三等分点,点F、G分别在线段PD、PC上.
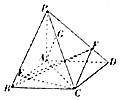
(Ⅰ)证明:CD⊥AG;
(Ⅱ)若三棱锥E-BCF的体积为
,求
的值.
| 2 |

(Ⅰ)证明:CD⊥AG;
(Ⅱ)若三棱锥E-BCF的体积为
| 1 |
| 6 |
| FD |
| PD |
▼优质解答
答案和解析
证明:(Ⅰ)∵棱锥P-ABCD的底面ABCD是平行四边形,PA=AB=AC=2,AD=2
,
∴AB2+AC2=BC2,∴AB⊥AC,
∵AB∥CD,∴AC⊥CD,
∵PA⊥平面ABCD,CD⊂平面ABCD,∴PA⊥CD,
∵AC∩PA=A,∴CD⊥平面PAC,
∵AG⊂平面PAC,∴CD⊥AG.
(Ⅱ)设点F到平面ABCD的距离为d,
S△BEC=
×2
×
=
,
∴由VE-BCF=VF-BEC=
S△BEC•d=
,
解得d=
,∴
=
=
.
| 2 |
∴AB2+AC2=BC2,∴AB⊥AC,
∵AB∥CD,∴AC⊥CD,
∵PA⊥平面ABCD,CD⊂平面ABCD,∴PA⊥CD,
∵AC∩PA=A,∴CD⊥平面PAC,
∵AG⊂平面PAC,∴CD⊥AG.
(Ⅱ)设点F到平面ABCD的距离为d,
S△BEC=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| 3 |
∴由VE-BCF=VF-BEC=
| 1 |
| 3 |
| 1 |
| 6 |
解得d=
| 3 |
| 4 |
| FD |
| PD |
| d |
| PA |
| 3 |
| 8 |
看了 已知四棱锥P-ABCD的底面...的网友还看了以下:
对于材料力学上的轴力图,外力作用点上的外力应该怎么理解?比如说下图C点,左边轴力是5P,右边是P, 2020-05-17 …
1.在平行四边形ABCD中,将E,F点分别从A,C点以相同速度向B,D点移动,将G,H点分别从A, 2020-05-20 …
数学课上,张老师给出了问题:如图(1),△ABC为等边三角形,动点D在边CA上,动点P边BC上,若 2020-06-15 …
根据地球公专示意图[图中左边是a点]南边是b点右边是c点北边是d点图中四点所表示的节气是?图中ab 2020-07-16 …
如图所示,AOB为一边界为1/4圆的匀强磁场,O点为圆心,D点为边界OB的中点,C点为边界上一点, 2020-07-20 …
探究题:如图:(1)△ABC为等边三角形,动点D在边CA上,动点P边BC上,若这两点分别从C、B点 2020-07-21 …
如图,平面直角坐标系中,已知A(-2,0),B(2,0),C(6,0),D为y轴正半轴上一点,且∠ 2020-07-22 …
如图所示,AOB为一个边界为四分之一圆的匀强磁场,O点为圆心,D点为边界OB的中点,C点为边界上一 2020-07-26 …
如图所示,AOB为一边界为14圆的匀强磁场,O点为圆心,D点为边界OE的中点,C点为边界上一点,且 2020-07-31 …
图所示,已知双曲线y=k/x(k>0)经过Rt△OAB的斜边OB的中点D,与直角边AB相交于点C,点 2020-11-27 …