早教吧作业答案频道 -->数学-->
探究题:如图:(1)△ABC为等边三角形,动点D在边CA上,动点P边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立
题目详情
探究题:如图:
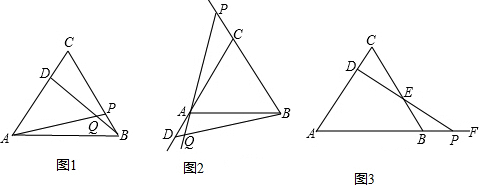
(1)△ABC为等边三角形,动点D在边CA上,动点P边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;
(2)如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条
件不变,如图(2)所示,两点运动过程中∠BQP的大小保持不变.请你利用图(2)的情形,
求证:∠BQP=60°;
(3)如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动,连接PD交BC于E”,其他条件不变,如图(3),则动点D,P在运动过程中,DE始终等于PE吗?写出证明过程.
(1)△ABC为等边三角形,动点D在边CA上,动点P边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;
(2)如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条
件不变,如图(2)所示,两点运动过程中∠BQP的大小保持不变.请你利用图(2)的情形,
求证:∠BQP=60°;
(3)如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动,连接PD交BC于E”,其他条件不变,如图(3),则动点D,P在运动过程中,DE始终等于PE吗?写出证明过程.

▼优质解答
答案和解析
考点:
全等三角形的判定与性质 等边三角形的判定与性质
专题:
分析:
(1)由△ABC为等边三角形,可得∠C=∠ABP=60°,AB=BC,又由这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,可得BP=CD,即可利用SAS,判定△ABP≌△BCD,继而证得结论;(2)同理可证得△ABP≌△BCD(SAS),则可得∠APB=∠BDC,然后由∠APB-∠PAC=∠ACB=60°,∠DAQ=∠PAC,求得∠BDC-∠DAQ=∠BQP=60°;(3)首先过点D作DG∥AB交BC于点G,则可证得△DCG为等边三角形,继而证得△DGE≌△PBE(AAS),则可证得结论.
(1)成立.理由:∵△ABC是等边三角形,∴∠C=∠ABP=60°,AB=BC,根据题意得:CD=BP,在△ABP和△BCD中,AB=BC∠ABP=∠CBP=CD,∴△ABP≌△BCD(SAS),∴AP=BD;(2)根据题意,CP=AD,∴CP+BC=AD+AC,即BP=CD,在△ABP和△BCD中,AB=BC∠ABP=∠BCDBP=CD,∴△ABP≌△BCD(SAS),∴∠APB=∠BDC,∵∠APB-∠PAC=∠ACB=60°,∠DAQ=∠PAC,∴∠BDC-∠DAQ=∠BQP=60°;(2)DE=PE.理由:过点D作DG∥AB交BC于点G,∴∠CDG=∠C=∠CGD=60°,∠GDE=∠BPE,∴△DCG为等边三角形,∴DG=CD=BP,在△DGE和△PBE中,∠DEG=∠PEB∠GDE=∠BPEDG=PB,∴△DGE≌△PBE(AAS),∴DE=PE.
点评:
此题考查了全等三角形的判定与性质以及等边三角形的性质.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
考点:
全等三角形的判定与性质 等边三角形的判定与性质
专题:
分析:
(1)由△ABC为等边三角形,可得∠C=∠ABP=60°,AB=BC,又由这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,可得BP=CD,即可利用SAS,判定△ABP≌△BCD,继而证得结论;(2)同理可证得△ABP≌△BCD(SAS),则可得∠APB=∠BDC,然后由∠APB-∠PAC=∠ACB=60°,∠DAQ=∠PAC,求得∠BDC-∠DAQ=∠BQP=60°;(3)首先过点D作DG∥AB交BC于点G,则可证得△DCG为等边三角形,继而证得△DGE≌△PBE(AAS),则可证得结论.
(1)成立.理由:∵△ABC是等边三角形,∴∠C=∠ABP=60°,AB=BC,根据题意得:CD=BP,在△ABP和△BCD中,AB=BC∠ABP=∠CBP=CD,∴△ABP≌△BCD(SAS),∴AP=BD;(2)根据题意,CP=AD,∴CP+BC=AD+AC,即BP=CD,在△ABP和△BCD中,AB=BC∠ABP=∠BCDBP=CD,∴△ABP≌△BCD(SAS),∴∠APB=∠BDC,∵∠APB-∠PAC=∠ACB=60°,∠DAQ=∠PAC,∴∠BDC-∠DAQ=∠BQP=60°;(2)DE=PE.理由:过点D作DG∥AB交BC于点G,∴∠CDG=∠C=∠CGD=60°,∠GDE=∠BPE,∴△DCG为等边三角形,∴DG=CD=BP,在△DGE和△PBE中,∠DEG=∠PEB∠GDE=∠BPEDG=PB,∴△DGE≌△PBE(AAS),∴DE=PE.
点评:
此题考查了全等三角形的判定与性质以及等边三角形的性质.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
看了 探究题:如图:(1)△ABC...的网友还看了以下:
在光滑的水平面上的物体,同时受到方向相反的两个力的作用,则该物体的运动状态( )在以下四个答案中选 2020-05-16 …
如图所示,A.B两长方体木块放在光滑水平面上,它们的高度相等,长木板C放在它们上面.用水平力F拉木 2020-05-17 …
关于水分在植物体内的运输,下列说法不正确的是A.通过导管,并沿着"叶--茎--根"的方向运输B.通 2020-06-14 …
某电路有一个灯泡和三个开关A,B,C.已知在且仅在下述四种情况下灯亮:(a)C的扳键向上,A,B的 2020-06-21 …
图中箭头表示植物体不同部位和不同条件下生长素的总体运输方向,下列据该图作出的判断不正确的是()A. 2020-07-04 …
高等数学中向量的叉积的内容向量a×b=a×c,则向量b=c么还是向量b-c垂直于a呢还是其他?、我 2020-07-30 …
某质点在一段时间内的位置-时间图象如图所示,关于0-t0时间内质点的运动情况,下列说法正确的是() 2020-07-31 …
高一向量两道小题,在线求解1、已知向量a,b,c满足a+b+c=0,模分别为a=1,b=√2,c= 2020-08-02 …
考察队员在南极大陆考察期间,看到太阳的运转方向是()A.东升西落B.太阳沿地平线按顺时针方向运转C. 2020-12-15 …
水分进入植物体以后的运输途径是()A.在导管和筛管中,沿着叶→茎→根的方向运输B.在筛管中,沿着叶→ 2021-01-13 …