早教吧作业答案频道 -->数学-->
如图,E、F是▱ABCD对角线AC上的两点,AF=CE.(1)求证:BE=DF;(2)若DF的延长线交BC于G,且点E、F是线段AC的三等分点,则GFFD=.
题目详情
如图,E、F是▱ABCD对角线AC上的两点,AF=CE.
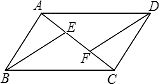
(1)求证:BE=DF;
(2)若DF的延长线交BC于G,且点E、F是线段AC的三等分点,则
=___.

(1)求证:BE=DF;
(2)若DF的延长线交BC于G,且点E、F是线段AC的三等分点,则
| GF |
| FD |
▼优质解答
答案和解析
(1)证明:∵AF=CE,
∴AF-EF=CE-EF.
∴AE=CF.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.AD∥BC,AD=BC,
∴∠BAE=∠DCF.
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS).
∴BE=DF;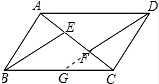
(2) 如图所示:由(1)得:△ABE≌△CDF,
∴∠AEB=∠DFC,
∴∠BEC=∠GFC,
∴BE∥GF,
∵点E、F是线段AC的三等分点,
∴AE=EF=FC,
∴BG=CG=
BC=
AD,
∵AD∥BC,
∴△CGF∽△ADF,
∴
=
=
;
故答案为:
.
∴AF-EF=CE-EF.
∴AE=CF.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.AD∥BC,AD=BC,
∴∠BAE=∠DCF.
在△ABE和△CDF中,
|
∴△ABE≌△CDF(SAS).
∴BE=DF;

(2) 如图所示:由(1)得:△ABE≌△CDF,
∴∠AEB=∠DFC,
∴∠BEC=∠GFC,
∴BE∥GF,
∵点E、F是线段AC的三等分点,
∴AE=EF=FC,
∴BG=CG=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD∥BC,
∴△CGF∽△ADF,
∴
| GF |
| FD |
| CG |
| AD |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
看了 如图,E、F是▱ABCD对角...的网友还看了以下:
如图,AC为圆O的直径,△ABD为圆O的内接三角形,AB=BD,BD交AC于F点,BE//AD交A 2020-04-27 …
如图所示,在三角形ABC中,角BAC=90度,AB=AC,角ACB的平分线交AB于D,过B作CD的 2020-05-16 …
已知BD是三角形ABC的一条中线,如果三角形ABD和三角形BCD周长是24,17.则AB-BC的长 2020-06-27 …
用两条平行线如何三等分一个圆 2020-06-30 …
在三角形ABc中,Lc>LB、AD是三角形ABc的一条角平分线如图一,AE垂直BC于E,试探究L在 2020-07-27 …
如图,bd是三角形abc的角平分线,de垂直ab,垂足为e.三角形abc的面积为70,ab=16, 2020-07-30 …
三角形AOB是等腰直角三角形,AB=2,动直线如图,三角形AOB是等腰直角三角形,AB的绝对值=2 2020-07-30 …
如何判定三点共线如题,三点共线的判定(平面几何) 2020-08-02 …
直线和射线的关系额.他说在作图.回答问题时候是不允许这样把线段说成直线的把.你只要说清两点1:找出图 2020-11-08 …
在三角形ABC中,AB=AC,BD是AC的中线,如果三角形ABC的周长为16厘米,且BD将三角形AB 2020-11-21 …