如图，在平面直角坐标系中，正比例函数y=kx（k>0）与反比例函数y=3x的图象分别交于A、C两点，已知点B与点D关于坐标原点O成中心对称，且点B的坐标为（m，0）．其中m&gt

Question

如图，在平面直角坐标系中，正比例函数y=kx（k>0）与反比例函数y= (3)/(x)的图象分别交于A、C两点，已知点B与点D关于坐标原点O成中心对称，且点B的坐标为（m，0）．其中m>0．

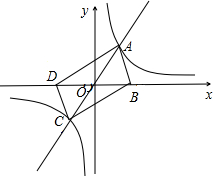
（1）四边形ABCD的是___．（填写四边形ABCD的形状）
（2）当点A的坐标为（n，3）时，四边形ABCD是矩形，求m，n的值．
（3）试探究：随着k与m的变化，四边形ABCD能不能成为菱形？若能，请直接写出k的值；若不能，请说明理由．

Answer 1

（1）∵正比例函数y=kx（k>0）与反比例函数y=(3)/(x)的图象分别交于A、C两点，
∴点A、C关于原点O成中心对称，
∵点B与点D关于坐标原点O成中心对称，
∴对角线BD、AC互相平分，
∴四边形ABCD的是平行四边形．
故答案为：平行四边形．
（2）∵点A（n，3）在反比例函数y=(3)/(x)的图象上，
∴3n=3，解得：n=1，
∴点A（1，3），
∴OA=√(10)．
∵四边形ABCD为矩形，
∴OA=(1)/(2)AC，OB=(1)/(2)BD，AC=BD，
∴OB=OA=√(10)，
∴m=√(10)．
（3）四边形ABCD不可能成为菱形，理由如下：
∵点A在第一象限内，点B在x轴正半轴上，
∴∠AOB<90°，
∴AC与BD不可能互相垂直，
∴四边形ABCD不可能成为菱形．