如图，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数y=kx（k≠0）的图象交于A、B两点，与x轴交于点C，过点A作AH⊥x轴于点H，点O是线段CH的中点，AC=45，cos∠ACH=55，点B的坐

Question

如图，在平面直角坐标系中，一次函数y=ax+b（a≠0）的图象与反比例函数y=(k)/(x)（k≠0）的图象交于A、B两点，与x轴交于点C，过点A作AH⊥x轴于点H，点O是线段CH的中点，AC=4√(5)，cos∠ACH=(√(5))/(5)，点B的坐标为（4，n）

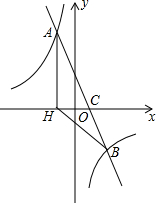
（1）求该反比例函数和一次函数的解析式；
（2）求△BCH的面积．

Answer 1

（1）∵AH⊥x轴于点H，AC=4√(5)，cos∠ACH=(√(5))/(5)，
∴(HC)/(AC)=(√(5))/(5)=(HC)/(4√(5))，
解得：HC=4，
∵点O是线段CH的中点，
∴HO=CO=2，
∴AH=√(AC2-HC2)=8，
∴A（-2，8），
∴反比例函数解析式为：y=-(16)/(x)，
∴B（4，-4），
∴设一次函数解析式为：y=kx+b，
则

-2k+b=8

4k+b=-4

，
解得：

k=-2

b=4

，
∴一次函数解析式为：y=-2x+4；

（2）由（1）得：△BCH的面积为：(1)/(2)×4×4=8．