已知点P是矩形ABCD内一点，连结AP、BP、CP、DP，若S△ABP+S△CDP=S△ADP+S△BCP，则关于点P的位置，正确的说法是（）A.一定是对角线交点B.一定在对角线上C.一定在对边中点的连线上D.可

Question

已知点P是矩形ABCD内一点，连结AP、BP、CP、DP，若S_△ABP+S_△CDP=S_△ADP+S_△BCP，则关于点P的位置，正确的说法是（　　）

A. 一定是对角线交点

B. 一定在对角线上

C. 一定在对边中点的连线上

D. 可以是任意位置

Answer 1

∵四边形ABCD是矩形，
∴AD=BC，AB=CD，
作PE⊥AD于E，延长EP交BC于F，如图所示：
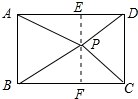
则PF⊥BC，EF=AB，
∵△ADP的面积+△BCP的面积=(1)/(2)AD•PE+(1)/(2)BC•PF=(1)/(2)BC（PE+PF）=(1)/(2)BC•EF=(1)/(2)BC•AB，
∴△ADP的面积+△BCP的面积=(1)/(2)矩形ABCD的面积，
同理：△ABP的面积+△CDP的面积=(1)/(2)矩形ABCD的面积，
∴△ADP的面积+△BCP的面积=△ABP的面积+△CDP的面积；
故选：D．