早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,∠BAC=45°,以AB为直径的⊙O交BC于点D,交AC于点E.(1)求∠EBC的度数;(2)求证:BD=CD.
题目详情
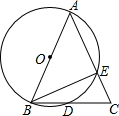 如图,在△ABC中,AB=AC,∠BAC=45°,以AB为直径的⊙O交BC于点D,交AC于点E.
如图,在△ABC中,AB=AC,∠BAC=45°,以AB为直径的⊙O交BC于点D,交AC于点E.(1)求∠EBC的度数;
(2)求证:BD=CD.
▼优质解答
答案和解析
考点:
圆周角定理 全等三角形的判定与性质 等腰三角形的性质
专题:
计算题
分析:
(1)根据等腰三角形的性质得∠ABC=∠C,再利用三角形内角和计算出∠C=12(180°-∠BAC)=67.5°,接着根据圆周角定理得∠AEB=90°,然后利用三角形外角性质求∠EBC的度数;(2)连结AD,如图,根据圆周角定理得∠ADB=90°,则AD⊥BC,然后根据等腰三角形的性质即可得到BD=CD.
(1)∵AB=AC,∴∠ABC=∠C,∴∠C=12(180°-∠BAC)=12(180°-45°)=67.5°,∵AB为直径,∴∠AEB=90°,∵∠AEB=∠EBC+∠C,∴∠EBC=90°-67.5°=22.5°;(2)证明:连结AD,如图,∵AB为直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,∴BD=CD.
点评:
本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的性质.
考点:
圆周角定理 全等三角形的判定与性质 等腰三角形的性质
专题:
计算题
分析:
(1)根据等腰三角形的性质得∠ABC=∠C,再利用三角形内角和计算出∠C=12(180°-∠BAC)=67.5°,接着根据圆周角定理得∠AEB=90°,然后利用三角形外角性质求∠EBC的度数;(2)连结AD,如图,根据圆周角定理得∠ADB=90°,则AD⊥BC,然后根据等腰三角形的性质即可得到BD=CD.
(1)∵AB=AC,∴∠ABC=∠C,∴∠C=12(180°-∠BAC)=12(180°-45°)=67.5°,∵AB为直径,∴∠AEB=90°,∵∠AEB=∠EBC+∠C,∴∠EBC=90°-67.5°=22.5°;(2)证明:连结AD,如图,∵AB为直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,∴BD=CD.
点评:
本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的性质.
看了 如图,在△ABC中,AB=A...的网友还看了以下:
同志们,求求你们了,帮我解决几道初二下学期的数学题,,△ABC=50°,∠ACB=80°,延长CB 2020-04-27 …
已知f(x)是定义在[-e,e]上的奇函数,当x€(0.e](€是属于符号)时,f(x)=e^x+ 2020-05-13 …
原函数是y=e^x,关于y=5对称 ,求对称后的表达式y= 原函数是y=e^x,关于x=1对称 , 2020-05-16 …
关于Excel:求C列数除以E列数的商乘以D列数的积的函数公式.注:1、C、E列有单位,如g、U、 2020-05-16 …
用C语言做以下题目,用最简单的语句哈,要不看不懂哈(0)设有十进制数字a,b,c,d和e,它们满足 2020-06-02 …
已知函数f(x)=Inx-x+1,x大于等于1,数列{an}满足a1=e,an+1/an=e(n为 2020-06-06 …
1.已知集合M={x|x=3n+1,n∈Z}.集合N={x|x=4n+3,n∈Z}.求M∩N2.设 2020-07-30 …
求一道集合问题的解法~设a,b是整数,集合E={(x,y)|(x-a)的平方+3b小于等于6y}点 2020-07-30 …
(1)正方形ABCD对角线为6根号2,点E是CD上一点,CE=2根号3,求角BED度数(2)正方形A 2020-12-25 …
关于隐函数求导(刚学)向各位博闻强识的前辈请教一个问题,在此先谢过,恕晚辈愚钝,对(e^y)+xy- 2021-01-01 …