早教吧作业答案频道 -->数学-->
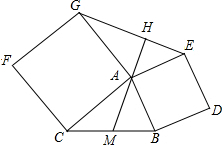
如图,在△ABC外分别以AB,AC为边作正方形ABDE和正方形ACFG,连接EG,AM是△ABC中BC边上的中线,延长MA交EG于点H,求证:(1)AM=12EG;(2)AH⊥EG;(3)EG2+BC2=2(AB2+AC2).
题目详情
如图,在△ABC外分别以AB,AC为边作正方形ABDE和正方形ACFG,连接EG,AM是△ABC中BC边上的中线,延长MA交EG于点H,求证:
(1)AM=
EG;
(2)AH⊥EG;
(3)EG2+BC2=2(AB2+AC2).

(1)AM=
| 1 |
| 2 |
(2)AH⊥EG;
(3)EG2+BC2=2(AB2+AC2).
▼优质解答
答案和解析
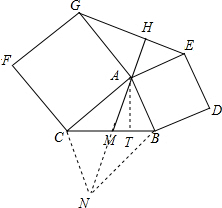
(1)证明:延长AM到点N,使MN=MA,连接BN,
∵AM是△ABC中BC边上的中线,
∴CM=BM,
在△MBN和△MCA中
∴△MBN≌△MCA(SAS),
∴∠BNM=∠CAM,NB=AC,
∴BN∥AC,NB=AG,
∴∠NBA+∠BAC=180°,
∵∠GAE+∠BAC=360°-90°-90°=180°,
∴∠NBA=∠GAE,
在△NBA和△GAE中
∴△NBA≌△GAE(SAS),
∴AN=EG,
∴AM=
EG;
(2)证明:由(1)△NBA≌△GAE得∠BAN=∠AEG,
∵∠HAE+∠BAN=180°-90°=90°,
∴∠HAE+∠AEH=90°,
∴∠AHE=90°,
即AH⊥EG;
(3)证明:作AT⊥BC于T,则BM=BT+TM,CM=CT-TM.
在Rt△ABT中,AB2=BT2+AT2,
在Rt△ACT中,AC2=CT2+AT2,
在Rt△ATM中,AT2=AM2-TM2,
∴AB2=BT2+AM2-TM2,
=AM2+BT2-TM2
=AM2+(BT+TM)(BT-TM)
=AM2+BM(BT-TM)①
AC2=CT2+AM2-TM2
=AM2+CT2-TM2
=AM2+(CT+TM)(CT-TM)
=AM2+CM(CT+TM)②
①+②得:AB2+AC2=2AM2+BM(BT-TM)+CM(CT+TM),
∵BM=CM,
∴AB2+AC2=2AM2+BM(BT-TM+CT+TM)
=2AM2+BM(BT+CT)
=2AM2+BM•BC
由(1)可知AM=
EG,
∵BM=
BC,
∴AB2+AC2=2(
EG)2+
BC•BC,
∴EG2+BC2=2(AB2+AC2).
∵AM是△ABC中BC边上的中线,
∴CM=BM,
在△MBN和△MCA中
|

∴△MBN≌△MCA(SAS),
∴∠BNM=∠CAM,NB=AC,
∴BN∥AC,NB=AG,
∴∠NBA+∠BAC=180°,
∵∠GAE+∠BAC=360°-90°-90°=180°,
∴∠NBA=∠GAE,
在△NBA和△GAE中
|
∴△NBA≌△GAE(SAS),
∴AN=EG,
∴AM=
| 1 |
| 2 |
(2)证明:由(1)△NBA≌△GAE得∠BAN=∠AEG,
∵∠HAE+∠BAN=180°-90°=90°,
∴∠HAE+∠AEH=90°,
∴∠AHE=90°,
即AH⊥EG;
(3)证明:作AT⊥BC于T,则BM=BT+TM,CM=CT-TM.
在Rt△ABT中,AB2=BT2+AT2,
在Rt△ACT中,AC2=CT2+AT2,
在Rt△ATM中,AT2=AM2-TM2,
∴AB2=BT2+AM2-TM2,
=AM2+BT2-TM2
=AM2+(BT+TM)(BT-TM)
=AM2+BM(BT-TM)①
AC2=CT2+AM2-TM2
=AM2+CT2-TM2
=AM2+(CT+TM)(CT-TM)
=AM2+CM(CT+TM)②
①+②得:AB2+AC2=2AM2+BM(BT-TM)+CM(CT+TM),
∵BM=CM,
∴AB2+AC2=2AM2+BM(BT-TM+CT+TM)
=2AM2+BM(BT+CT)
=2AM2+BM•BC
由(1)可知AM=
| 1 |
| 2 |
∵BM=
| 1 |
| 2 |
∴AB2+AC2=2(
| 1 |
| 2 |
| 1 |
| 2 |
∴EG2+BC2=2(AB2+AC2).
看了 如图,在△ABC外分别以AB...的网友还看了以下:
任意三角形三等分点连线形成的三角形与大三角形的面积比 2020-04-26 …
英语翻译百慕大三角的具体地理位置是指位于大西洋上的百慕大群岛、迈阿密(美国佛罗里达半岛)和圣胡安( 2020-05-14 …
如何用几何画板描点法画一图形就是我标出了了很多个点,然后想把它们连点成线 形成一个图形然后又开始画 2020-05-16 …
如图,四边形ABCD是正方形,点G是BC上任意一点,DE垂直AB于点E,BF垂直AG于点F,当点G 2020-05-17 …
麻烦的几何题三角形ABC,M为BC边的中点,G为三角形的重心.G'为点G通过点M的对称点,D为AB 2020-06-03 …
四边形ABCD是平行四边形,E是对角线AC上一点,射线DE分别交射线CB、AB于点F、G.(1)如 2020-06-12 …
(2014•盘锦)已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方 2020-06-13 …
△ABC内有任意三点不共线的2008个点,加上A,B,C三个顶点,共2011个点,将这2011个点 2020-07-31 …
△ABC内有任意三点都不共线的2011个点,加上A,B,C三个顶点,共2014个点,把这2014个 2020-07-31 …
如图,四边形ABCD是正方形,点G是直线BC上的任意一点,DE⊥AG于点E,BF∥DE,交AG于F. 2020-12-25 …