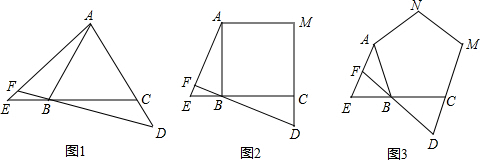
如图1、图2、图3中，点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的一边延长线和另一边反向延长线上的点，且△ABE与△BCD能互相重合，BD延长线交AE于点F．（1）求图1中，

Question

如图1、图2、图3中，点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的一边延长线和另一边反向延长线上的点，且△ABE与△BCD能互相重合，BD延长线交AE于点F．
（1）求图1中，∠AFB的度数；
（2）图2中，∠AFB的度数为___，图3中，∠AFB的度数为___．

Answer 1

（1）∵△ABE与△BCD能互相重合，
∴∠D=∠E，
∵∠DBC=∠EBF，
∴∠BFE=180°-∠E-∠EBF=180°-∠D-∠B=∠BCD．
∵∠BCD+∠ACB=180°，∠ACB=60°，∠AFB+∠BFE=180°，
∴∠AFB=∠ACB=60°．
（2）同理可得出：∠AFB=∠BCM，
∵四边形ABCD为正方形，五边形ABCMN为正五边形，
∴图2中∠BCM=90°，图3中∠BCM=108°．
故答案为：90°；108°．