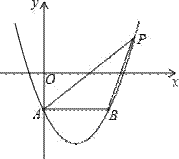
如图，在平面直角坐标系中，抛物线y=x2﹣2x﹣1交y轴于点A，过点A作AB∥x轴交抛物线于点B，点P在抛物线上，连结PA、PB，若点P关于x轴的对称点恰好落在直线AB上，则△ABP的面积是．

Question

如图，在平面直角坐标系中，抛物线y=x²﹣2x﹣1交y轴于点A，过点A作AB∥x轴交抛物线于点B，点P在抛物线上，连结PA、PB，若点P关于x轴的对称点恰好落在直线AB上，则△ABP的面积是　　．

Answer 1

2【考点】二次函数图象上点的坐标特征．

【分析】求得C的坐标，进而求得B的坐标，根据点P关于x轴的对称点恰好落在直线AB上得出三角形的高，然后根据三角形面积公式即可求得．

【解答】令x=0，则y=x²﹣2x﹣1=﹣1，

∴A（0，﹣1），

把y=﹣1代入y=x²﹣2x﹣1得﹣1=x²﹣2x﹣1，

解得x₁=0，x₂=2，

∴B（2，﹣1），

∴AB=2，

∵点P关于x轴的对称点恰好落在直线AB上，

∴△PAB边AB上的高为2，

∴S=×2×2=2．

故答案为2．

【点评】本题考查了二次函数图象上点的坐标特征，求得A、B的坐标以及三角形的高是解题的关键．