早教吧作业答案频道 -->数学-->
(1)问题发现:如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.请把下面的证明过程补充完整:证明:过点E作EF∥AB,∵AB∥DC(已知),EF∥AB(辅助线的作法
题目详情
(1)问题发现:如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.
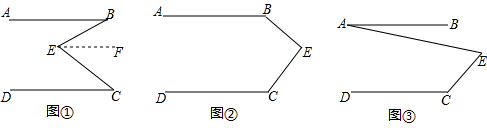
请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法).
∴EF∥DC(___).
∴∠C=∠CEF(___)
∵EF∥AB,∴∠B=∠BEF(同理).
∴∠B+∠C=___(等量代换)
即∠B+∠C=∠BEC.
(2)拓展探究:如果点E运动到图②所示的位置,其他条件不变,进一步探究发现:∠B+∠C=360°-∠BEC,请说明理由.
(3)解决问题:如图③,AB∥DC,∠C=120°,∠AEC=80°,请直接写出∠A的度数.

请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法).
∴EF∥DC(___).
∴∠C=∠CEF(___)
∵EF∥AB,∴∠B=∠BEF(同理).
∴∠B+∠C=___(等量代换)
即∠B+∠C=∠BEC.
(2)拓展探究:如果点E运动到图②所示的位置,其他条件不变,进一步探究发现:∠B+∠C=360°-∠BEC,请说明理由.
(3)解决问题:如图③,AB∥DC,∠C=120°,∠AEC=80°,请直接写出∠A的度数.
▼优质解答
答案和解析
(1)根据平行公理,平行线的性质可知;
平行于同一直线的两直线平行,
两直线平行,内错角相等,
∠BEF+∠CEF;
(2)过点E作EF∥AB,
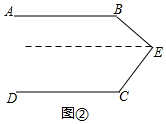 ∵AB∥DC,EF∥AB,
∵AB∥DC,EF∥AB,
∴EF∥DC,
∴∠C+∠CEF=180°,∠B+∠BEF=180°,
∴∠B+∠C+∠AEC=360°,
∴∠B+∠C=360°-∠BEC;
(3)连接BE,
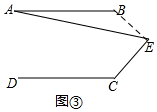 由(2)可知:∠B+∠C=360°-∠BEC;
由(2)可知:∠B+∠C=360°-∠BEC;
∴∠B+∠BEC=360°-120°=240°,
∴∠B+∠AEB+∠AEC=240°,
∴∠B+∠AEB=160°,
∴∠A=180°-(∠B+∠AEB)=20°
故答案为:(1)平行于同一直线的两直线平行;两直线平行,内错角相等;∠BEF+∠CEF;
平行于同一直线的两直线平行,
两直线平行,内错角相等,
∠BEF+∠CEF;
(2)过点E作EF∥AB,
 ∵AB∥DC,EF∥AB,
∵AB∥DC,EF∥AB,∴EF∥DC,
∴∠C+∠CEF=180°,∠B+∠BEF=180°,
∴∠B+∠C+∠AEC=360°,
∴∠B+∠C=360°-∠BEC;
(3)连接BE,
 由(2)可知:∠B+∠C=360°-∠BEC;
由(2)可知:∠B+∠C=360°-∠BEC;∴∠B+∠BEC=360°-120°=240°,
∴∠B+∠AEB+∠AEC=240°,
∴∠B+∠AEB=160°,
∴∠A=180°-(∠B+∠AEB)=20°
故答案为:(1)平行于同一直线的两直线平行;两直线平行,内错角相等;∠BEF+∠CEF;
看了 (1)问题发现:如图①,直线...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
基本不等式超费解130已知a>b>0,求a2+1/(a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
设a>0,f(x)=e^x/a+a/e^x是R上的偶函数,求a值.∵f(x)=e^x/a+a/e^ 2020-05-17 …
用以下英文宇母填在上a,a,a,a,a,a,b,e,e,d,e,e,e,e,e,e,f,g,g用以 2020-06-24 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
矩阵平方差设方阵A满足A²-A-2E=O,求A的逆矩阵.答案是1/2(A-E).为啥不是1/2E, 2020-07-18 …
线性代数矩阵A满足A*=A^T,如a11,a12,a13为三个相等的正数,则a11为多少?由AA* 2020-07-25 …
已知向量a≠e,|e|=1,满足:任意t∈R.已知向量a不等于e,|e|=1,对任意t属于R,恒有 2020-07-25 …
递回关系式的运算公式(数列)以下是推导一个公式"a=a+r(1-p^n)/(1-p)"的过程a=p* 2021-01-13 …