早教吧作业答案频道 -->数学-->
已知函数f(x)=inx-a(x-1),a∈R(Ⅰ)讨论函数f(x)的单调性;(Ⅱ)当x≥1时,f(x)≤恒成立,求a的取值范围.
题目详情
已知函数f(x)=inx-a(x-1),a∈R
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)当x≥1时,f(x)≤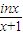 恒成立,求a的取值范围.
恒成立,求a的取值范围.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)当x≥1时,f(x)≤
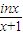 恒成立,求a的取值范围.
恒成立,求a的取值范围.▼优质解答
答案和解析
分析:
(Ⅰ)f(x)的定义域为(0,+∞),,若a≤0,f(x)在(0,+∞)上单调递增;若a>0时,f(x)在(0,)上单调递增,在(,+∞)单调递减.(Ⅱ)f(x)-=,令g(x)=xlnx-a(x2-1),(x≥1),g′(x)=lnx+1-2ax,令F(x)=g′(x)=lnx+1-2ax,,由此进行分类讨论,能求出实数a的取值范围.
(本小题满分12分)(Ⅰ)f(x)的定义域为(0,+∞),,若a≤0,则f′(x)>0,∴f(x)在(0,+∞)上单调递增,…(2分)若a>0,则由f′(x)=0,得x=,当x∈(0,)时,f′(x)>0,当x∈()时,f′(x)<0,∴f(x)在(0,)上单调递增,在(,+∞)单调递减.所以当a≤0时,f(x)在(0,+∞)上单调递增,当a>0时,f(x)在(0,)上单调递增,在(,+∞)单调递减.…(4分)(Ⅱ)f(x)-=,令g(x)=xlnx-a(x2-1),(x≥1),g′(x)=lnx+1-2ax,令F(x)=g′(x)=lnx+1-2ax,,…(6分)①或a≤0,F′(x)>0,g′(x)在[1,+∞)递增,g′(x)≥g′(1)=1-2a>0,∴g(x)在[1,+∞)递增,g(x)≥g(1)=0,从而f(x)-不符合题意.…(8分)②若0<a<,当x∈(1,),F′(x)>0,∴g′(x)在(1,)递增,从而g′(x)>g′(1)=1-2a,∴g(x)在[1,+∞)递增,g(x)≥g(1)=0,从而f(x)-不符合题意.…(10分)③若a,F′(x)≤0在[1,+∞)恒成立,∴g′(x)在[1,+∞)递减,g′(x)≤g′(1)=1-2a≤0,从而g9x)在[1,+∞)递减,∴g(x)≤g(1)=0,f(x)-≤0,综上所述,a的取值范围是[).…(12分)
点评:
本题考查函数的单调性的求法,考查满足条件的实数的取值范围的求法.综合性强,难度大,有一定的探索性,对数学思维的要求较高,解题时要注意导数性质的合理运用.
分析:
(Ⅰ)f(x)的定义域为(0,+∞),,若a≤0,f(x)在(0,+∞)上单调递增;若a>0时,f(x)在(0,)上单调递增,在(,+∞)单调递减.(Ⅱ)f(x)-=,令g(x)=xlnx-a(x2-1),(x≥1),g′(x)=lnx+1-2ax,令F(x)=g′(x)=lnx+1-2ax,,由此进行分类讨论,能求出实数a的取值范围.
(本小题满分12分)(Ⅰ)f(x)的定义域为(0,+∞),,若a≤0,则f′(x)>0,∴f(x)在(0,+∞)上单调递增,…(2分)若a>0,则由f′(x)=0,得x=,当x∈(0,)时,f′(x)>0,当x∈()时,f′(x)<0,∴f(x)在(0,)上单调递增,在(,+∞)单调递减.所以当a≤0时,f(x)在(0,+∞)上单调递增,当a>0时,f(x)在(0,)上单调递增,在(,+∞)单调递减.…(4分)(Ⅱ)f(x)-=,令g(x)=xlnx-a(x2-1),(x≥1),g′(x)=lnx+1-2ax,令F(x)=g′(x)=lnx+1-2ax,,…(6分)①或a≤0,F′(x)>0,g′(x)在[1,+∞)递增,g′(x)≥g′(1)=1-2a>0,∴g(x)在[1,+∞)递增,g(x)≥g(1)=0,从而f(x)-不符合题意.…(8分)②若0<a<,当x∈(1,),F′(x)>0,∴g′(x)在(1,)递增,从而g′(x)>g′(1)=1-2a,∴g(x)在[1,+∞)递增,g(x)≥g(1)=0,从而f(x)-不符合题意.…(10分)③若a,F′(x)≤0在[1,+∞)恒成立,∴g′(x)在[1,+∞)递减,g′(x)≤g′(1)=1-2a≤0,从而g9x)在[1,+∞)递减,∴g(x)≤g(1)=0,f(x)-≤0,综上所述,a的取值范围是[).…(12分)
点评:
本题考查函数的单调性的求法,考查满足条件的实数的取值范围的求法.综合性强,难度大,有一定的探索性,对数学思维的要求较高,解题时要注意导数性质的合理运用.
看了 已知函数f(x)=inx-a...的网友还看了以下:
spss中回归分析实例求助,这样的R值F值T值可以继续做下去吗?R^2=0.734F=80.181 2020-04-05 …
一道高一二次函数题设二次函数f(x)=ax²+bx+c(a,b,c∈R)满足下列条件:1>当x∈R 2020-05-20 …
f(x)=x^2+|x-a|+1,x属于R,常数a为R,求f(x)最小值问过一次,还有疑问,上次答 2020-05-23 …
f(x)是定义在R上的函数,且对任意实数x,y都有f(x+y)=f(x)+f(y)-1成立,当f( 2020-06-02 …
已知定义在R+上的函数f(x)同时满足下列三个条件:f(3)=-1;对任意x、y属于R+,都有f( 2020-06-03 …
方差分析时,F值与F0.05、F0.01相比较大小,得到的结果有什么意义?若F大于等于F0.05或 2020-06-10 …
设定义在R上的函数f(x)=a4x^2+a3x^3+a2x^2+a1x+a0的图像关于原点对称,且 2020-07-09 …
1、设偶函数f(x)对任意x属于R,都有f(x+3)=-f(x)分之1,且当x属于-3,-2时,则 2020-07-18 …
已知函数f(x)的定义域为R,对任意的x,y∈R,都有f(x+y)=f(x)*f(y)当x>0时, 2020-07-22 …
高一数学函数定义在实数集R上的函数Y=F(X)是偶函数,当X大于等于0时,F(X)=-4X平方+8X 2020-12-08 …