早教吧作业答案频道 -->物理-->
在同一竖直面内的同一水平线上A、B两点分别以30°、60°为发射角同时抛出两球,欲使两小球相遇时都在自己的轨道的最高点,已知小球在一点的发射速度VAO=9.8米/秒,求VBO和A、B两点间的距
题目详情
在同一竖直面内的同一水平线上A、B两点分别以30°、60°为发射角同时抛出两球,欲使两小球相遇时都在自己的轨道的最高点,已知小球在一点的发射速度VAO=9.8米/秒,求VBO和A、B两点间的距离.(g取9.8m/s2,结果保留两位小数)
▼优质解答
答案和解析
以A点为原点建立图示坐标系,取发射时刻为计时起点,两点间距离为S,初始条件如图所示.
据斜抛规律有: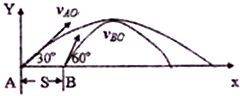
xA=vOcos30°t (1)
xB=vBOcos60°t+S (2)
vAy=vAOsin30°-gt (3)
vBy=vBOsin60°-gt (4)
满足题中条件,在最高点相遇,必有vAy=vBy=0,xA=xB
令(3)、(4)为零;
则有:t=
(5)
vBO=vAOsin30
(6)
代入数据可得:vBO=5.66m/s;
令(1)=(2)得S=(vAOcos30°-0.5cos60°)t (7)
将(5)、(6)代入(7)可得:
S=
(cos30°-0.5cos60°)=2.83m;
答:VBO为5.66m/s;A、B两点间的距离为2.83m
据斜抛规律有:

xA=vOcos30°t (1)
xB=vBOcos60°t+S (2)
vAy=vAOsin30°-gt (3)
vBy=vBOsin60°-gt (4)
满足题中条件,在最高点相遇,必有vAy=vBy=0,xA=xB
令(3)、(4)为零;
则有:t=
| vAOsin30° |
| g |
vBO=vAOsin30
| vBOsin30° |
| sin60° |
代入数据可得:vBO=5.66m/s;
令(1)=(2)得S=(vAOcos30°-0.5cos60°)t (7)
将(5)、(6)代入(7)可得:
S=
| ||
| 2g |
答:VBO为5.66m/s;A、B两点间的距离为2.83m
看了 在同一竖直面内的同一水平线上...的网友还看了以下:
设M(a,0)是抛物线y^2=2px对称轴上的一个定点,过M的直线交抛物线于A,B两点,其纵坐标分 2020-05-16 …
如图,在直角坐标系中,抛物线y=ax^2+bx+c(a不等于0)与x轴交于点A(-1,0),B(3 2020-05-16 …
谁知道二次函数中“aπ0”、“aφ0”二次函数y=ax2+bx+c图像、填表中、分为了“aπ0”、 2020-06-12 …
1.设直线y=x/2+3交两坐标轴于A.B两点,平移抛物线y=-x^2/4,使其过A,B两点,求平 2020-06-14 …
函数y=ae^bx(a>0)两边取对数得lny=ln(ae^bx)怎么推出lny=lna+bx本人 2020-07-03 …
若方程x2-11x+30+a=0两根都大于5,则实数a的取值范围是. 2020-07-21 …
如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,-1)的抛物线y=ax²+bx+c(a 2020-07-29 …
一个数学题过X轴上的动点A(a,0),向抛物线y=x^2+1引两切线,AP,AQ,P,Q为切点,1 2020-07-30 …
根号a(a≥0)表示a的算数平方根,试就a>0和a=0两种情况,分别说出它的意义书本上的题. 2020-08-03 …
(2004•龙岩)如图,已知抛物线C:y=-12x2+12x+3与x轴交于点A、B两点,过定点的直线 2020-11-12 …