早教吧作业答案频道 -->数学-->
若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界
题目详情
若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任一两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.
例如:下面所表示的函数的界高为4.
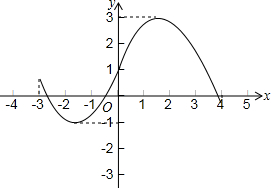
(1)若函数y=kx+1(-2≤x≤1)的界高为4,求k的值;
(2)已知m>-2,若函数y=x2(-2≤x≤m)的界高为4,求实数m的取值范围;
(3)已知a>0,函数y=x2-2ax+3a(-2≤x≤1)的界高为
,求a的值.
例如:下面所表示的函数的界高为4.
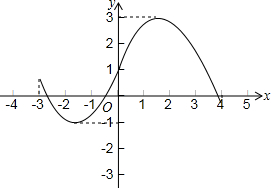
(1)若函数y=kx+1(-2≤x≤1)的界高为4,求k的值;
(2)已知m>-2,若函数y=x2(-2≤x≤m)的界高为4,求实数m的取值范围;
(3)已知a>0,函数y=x2-2ax+3a(-2≤x≤1)的界高为
| 25 |
| 4 |
▼优质解答
答案和解析
(1)将x1=-2代入得;y1=-2k+1,将x2=1代入得:y2=k+1,
∵|y1-y2|=4,
∴|-3k|=4.
解得:k=±
.
(2)将y=4代入抛物线的解析式得:x2=4,解得:x1=-2,x2=2,
∴m=2.
∴m的取值范围是0≤m<2.
(3)当a≥1时,将x1=-2,x2=1代入函数解析式求得y1=4+7a,y2=1+a,
∵|y1-y2|=
,
∴3+6a=
,
解得:a=
又∵a≥1
故此种情况不成立;
当0≤a≤1时,将x1=-2,x2=a代入函数解析式得:y1=4+7a,y2=3a-a2,
∵y1-y2=
,
∴a2+4a-
=0,
解得:a1=
,a2=-
(舍去)
故a=
.
∵|y1-y2|=4,
∴|-3k|=4.
解得:k=±
| 4 |
| 3 |
(2)将y=4代入抛物线的解析式得:x2=4,解得:x1=-2,x2=2,
∴m=2.
∴m的取值范围是0≤m<2.
(3)当a≥1时,将x1=-2,x2=1代入函数解析式求得y1=4+7a,y2=1+a,
∵|y1-y2|=
| 25 |
| 4 |
∴3+6a=
| 25 |
| 4 |
解得:a=
| 13 |
| 24 |
又∵a≥1
故此种情况不成立;
当0≤a≤1时,将x1=-2,x2=a代入函数解析式得:y1=4+7a,y2=3a-a2,
∵y1-y2=
| 25 |
| 4 |
∴a2+4a-
| 9 |
| 4 |
解得:a1=
| 1 |
| 2 |
| 9 |
| 2 |
故a=
| 1 |
| 2 |
看了 若y是关于x的函数,H是常数...的网友还看了以下:
立体图形工地上放着两根质地相同的圆柱形木料,它们长度相等,甲的底面半径是乙的2倍,队长让技术员称一 2020-05-13 …
已知关于x的一元二次方程(k-1)x^2+(2k+2)x+k=0有两个不相等的实数根(1)求实数k 2020-05-16 …
已知抛物线Y=-X*2+4交X轴于A,B两点,顶点是C.1.求三角形ABC的面积.2若点P在Y=- 2020-06-14 …
整数1至50构成集合M,从中任取25个数构成集合N,输入a,b,c,d,e,六个数,判断是否属于N 2020-06-28 …
有个excel函数问题想请教、当B1>0时候判定A1是否大于0若大于0则H1等于0若小于0则等于1 2020-07-30 …
集合A={x|x^2-(t^2+t+1)x+t(t^2+1)>0},B={x|x=1/2m^2-m 2020-08-02 …
①设a,b为2条直线,α,β为两个平面,下列四个命题中正确的是()A若a.b与α所成的角相等,则a平 2020-11-02 …
13.辛亥革命之前,“太太”一直用于称呼官员的妻子;而民国时期,“太太”成为上流社会和平民百姓共同青 2020-11-23 …
辛亥革命之前,“太太”一直用于称呼官员的妻子;而民国时期,“太太”成为上流社会和平民百姓共同青睐的称 2020-11-23 …
设a,b是两个非零向量.A若/a+b/=/a/-/b/,则a垂直于bB若a垂直于b,则/a+b/=/ 2021-02-05 …