早教吧作业答案频道 -->数学-->
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.(Ⅰ)证明:平面PAD⊥平面ABFE;(Ⅱ)求正四棱锥P-ABCD的高h,使得该四棱锥的体积是三棱锥P-ABF
题目详情
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.
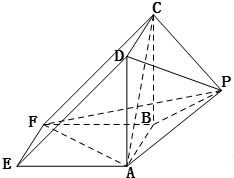
(Ⅰ)证明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱锥P-ABCD的高h,使得该四棱锥的体积是三棱锥P-ABF体积的4倍.

(Ⅰ)证明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱锥P-ABCD的高h,使得该四棱锥的体积是三棱锥P-ABF体积的4倍.
▼优质解答
答案和解析
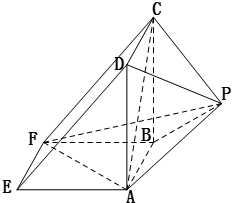 (Ⅰ)证明:直三棱柱ADE-BCF中,AB⊥平面ADE,
(Ⅰ)证明:直三棱柱ADE-BCF中,AB⊥平面ADE,
所以:AB⊥AD,又AD⊥AF,
所以:AD⊥平面ABFE,AD⊂平面PAD,
所以:平面PAD⊥平面ABFE….(6分)
(Ⅱ)P到平面ABCD的距离d=1
所以:VP-ABF=
S△ABFd=
×
×2×2×1=
而:VP-ABCD=
SABCDh=
×2×2h=4VP-ABF=
,
所以h=2….(12分)
 (Ⅰ)证明:直三棱柱ADE-BCF中,AB⊥平面ADE,
(Ⅰ)证明:直三棱柱ADE-BCF中,AB⊥平面ADE,所以:AB⊥AD,又AD⊥AF,
所以:AD⊥平面ABFE,AD⊂平面PAD,
所以:平面PAD⊥平面ABFE….(6分)
(Ⅱ)P到平面ABCD的距离d=1
所以:VP-ABF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
而:VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
所以h=2….(12分)
看了 如图所示,该几何体是由一个直...的网友还看了以下:
将一块含30度角的三角尺绕直角边旋转一周得到一个圆锥、这个圆锥的高是4,则圆锥的侧面积是多少,请写 2020-04-13 …
在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE且BC=2,若此正三棱锥的四个顶点 2020-04-24 …
在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE且BC=2,若此正三棱锥的四个顶点 2020-04-24 …
圆柱圆锥问题一个底面积是9.6平方米,高是1米的圆柱体钢胚熔铸成和它相等的圆锥体,每个圆锥体体积是 2020-04-26 …
一个圆锥与一个圆柱的底面积相等.已知圆锥与圆柱的休积的比是1/6,圆锥的高是4.8厘米,求圆柱的高 2020-05-20 …
正方形ABCD的边长为23,以A为圆心作弧EF交AB于E,圆O与EF切于G,与BC.CD都相切.若 2020-06-03 …
有一个所有棱长均为a的正四棱锥P-ABCD,还有一个所有棱长均为a的正三棱锥,将此三棱锥的一个面与 2020-06-27 …
在一个圆锥高的2分之1处把圆锥截成一个小圆锥和一个圆台两部分,已知小圆锥的底面半径是大圆锥底面半径 2020-07-25 …
如图所示,两个悬于同一悬点O,且在同一水平面内做匀速圆周运动的圆锥摆e和f,它们的质量相等,摆线长 2020-07-31 …
我们将侧棱和底面边统称为棱,则三棱锥有4个面,6条棱,4个顶点,如果面数记作F,棱数记作E,顶点数记 2020-11-18 …