已知定点A(a，0)，动点P对极点O和点A的张角，在OP的延长线上取点Q，使|PQ|=|PA|．当P在极轴上方运动时，求点Q的轨迹的极坐标方程．
已知定点 A(a ， 0) ，动点 P 对极点 O 和点 A 的张角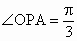 
，在 OP 的延长线上取点 Q ，使 |PQ|=|PA| ．当 P 在极轴上方运动时，求点 Q 的轨迹的极坐标方程．
解析：
设Q、P的坐标分别是(ρ，θ)，，则． 在△POA中，，． 又|OQ|=|OP|＋|PA|，∴．
如图，PA，PB切O于A，B两点，CD切O于点E，交PA，PB于C，D．延长BO交PA的延长线于点 2020-04-12 …
如图，已知AB为⊙O的直径，PA，PC是⊙O的切线，A，C为切点，∠BAC=30°．（Ⅰ）求∠P的 2020-05-16 …
以知以原点为圆心的圆O在直线x-y-2=0上截得的玄长为2倍根号下2.1.求圆O的方程2.若圆O与 2020-07-02 …
边长为2的正方形ABCD内有一点P,求PA+PB+PC的最小值.请写出过程.7.AB边长为2的正方 2020-07-20 …
已知PO是平面α的垂线,O为垂足,PO=6,PA,PB,PC是平面α的斜线,A,B,C是斜足已知P 2020-07-30 …
如图，点O在∠APB的平分线上，⊙O与PA相切于点C．（1）求证：直线PB与⊙O相切；（2）PO的 2020-07-31 …
如图，已知AB为⊙O的直径，PA与⊙O相切于点A，线段OP与弦AC垂直并相交于点D，OP与弧AC相 2020-07-31 …
如图，正方形ABCD边长为2，内切圆为⊙O，点P是⊙O上任意一点．（1）求|PA+PB+PC+PD 2020-07-31 …
高中立体几何4半径为r的圆O在平面@内,正三角形ABC内接于圆O,平面@外一点P在@内的射影是O点 2020-08-02 …
点O在∠APB的平分线上,圆O与PA相切与点C,求证PB与圆O相切点A、P、B均是圆O的点，连接AP 2021-01-11 …