早教吧作业答案频道 -->数学-->
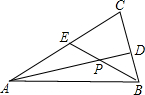
如图,△ABC的角平分线AD、BE相交于点P.∠ABC是直角,∠C=60°,请你判断并写出PE与PD之间的数量关系,并说明理由.
题目详情
如图,△ABC的角平分线AD、BE相交于点P.∠ABC是直角,∠C=60°,请你判断并写出PE与PD之间的数量关系,并说明理由.

▼优质解答
答案和解析
PE=PD.
证明:∵∠ABC=90°,∠C=60°,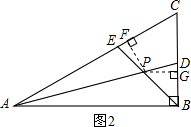
∴∠CAB=30°,
∵AD平分∠BAC,BE平分∠ABC,
∴∠CAD=∠BAD=
∠CAB=15°,∠ABE=∠CBE=
∠ABC=45°,
过点P作PF⊥AC,PG⊥BC,垂足分别为F、G,
则∠PFE=∠PGD=90°,
∵∠PDG为△ADC的一个外角,
∴∠PDG=∠C+∠CAD=60°+
∠CAB=60°+15°=75°,
∵∠PEF是△ABE的一个外角,
∴∠PEF=∠CAB+∠ABE=30°+
∠CBA=30°+45°=75°,
∴∠PEF=∠PDG,
∵PF⊥AC,PG⊥BC,
∴∠PFE=∠PGD=90°,
根据角平分线的性质可知:PF=PG,
在△PFE和△PGD中,
∴△PFE≌△PGD,
∴PE=PD.
证明:∵∠ABC=90°,∠C=60°,

∴∠CAB=30°,
∵AD平分∠BAC,BE平分∠ABC,
∴∠CAD=∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
过点P作PF⊥AC,PG⊥BC,垂足分别为F、G,
则∠PFE=∠PGD=90°,
∵∠PDG为△ADC的一个外角,
∴∠PDG=∠C+∠CAD=60°+
| 1 |
| 2 |
∵∠PEF是△ABE的一个外角,
∴∠PEF=∠CAB+∠ABE=30°+
| 1 |
| 2 |
∴∠PEF=∠PDG,
∵PF⊥AC,PG⊥BC,
∴∠PFE=∠PGD=90°,
根据角平分线的性质可知:PF=PG,
在△PFE和△PGD中,
|
∴△PFE≌△PGD,
∴PE=PD.
看了 如图,△ABC的角平分线AD...的网友还看了以下:
水平放置的△ABC的直观图为△A′B′C′,A′B′∥y′轴,B′C′在x′轴上,则△ABC是() 2020-06-27 …
已知a,b,c是△ABC的三边长,如果(c-5)2+|b-12|+a2−26a+169=0,则△A 2020-07-18 …
如图,在7×4的网格上有一个△ABC(A、B、C分别在小正方形的顶点上).若每个小正方形的边长都为 2020-07-20 …
设A,B,C,D是空间内不公面的四点,且满足,则是设A,B,C,D是空间内不公面的四点,且满足向量 2020-07-22 …
已知a,b,c是三角形的三边长,如果满足(a-b)2+b−8+|c2-64|=0,则三角形的形状是 2020-07-23 …
三角形三边长a、b、c满足(a-b-c)(b-c)=0,则这个三角形是()A.等边三角形B.等腰三 2020-08-02 …
把△ABC按斜二测画法得到△A′B′C′(如图所示),其中B′O′=C′O′=1,A′O′=32, 2020-08-02 …
在△ABC中,∠A=2∠B=3∠C,可以判断该三角形的形状是()A.直角三角形B.锐角三角形C.钝 2020-08-03 …
在△ABC中,角A,B,C的对边分别为a,b,c,其中c边最长,并且sin2A+sin2B=1,则 2020-08-03 …
(2011•南充一模)若集合S={a,b,c}(a、b、c∈R)中三个元素为边可构成一个三角形,那么 2020-11-12 …