早教吧作业答案频道 -->数学-->
(1)如图1,在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O.求证:OA=OE.(2)如图2,AB是O的直径,AC是O的弦,过点B作O的切线DE,与AC的延长线交于点D,作AE⊥AC
题目详情
(1)如图1,在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O.求证:OA=OE.
(2)如图2,AB是 O的直径,AC是 O的弦,过点B作 O的切线DE,与AC的延长线交于点D,作AE⊥AC交DE于点E.求证:∠BAD=∠E.
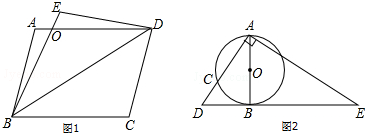
(2)如图2,AB是 O的直径,AC是 O的弦,过点B作 O的切线DE,与AC的延长线交于点D,作AE⊥AC交DE于点E.求证:∠BAD=∠E.

▼优质解答
答案和解析
(1)证明:平行四边形ABCD中,将△BCD沿BD对折,使点C落在E处,
可得∠DBE=∠ADB,∠A=∠C,
∴OB=OD,
在△AOB和△EOD中,
,
∴△AOB≌△EOD(AAS),
∴OA=OE.
(2)证明:∵AB是 O的直径,AC是 O的弦,过点B作 O的切线DE,
∴∠ABE=90°,
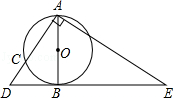
∴∠BAE+∠E=90°,
∵∠DAE=90°,
∴∠BAD+∠BAE=90°,
∴∠BAD=∠E.
可得∠DBE=∠ADB,∠A=∠C,
∴OB=OD,
在△AOB和△EOD中,
|
∴△AOB≌△EOD(AAS),
∴OA=OE.
(2)证明:∵AB是 O的直径,AC是 O的弦,过点B作 O的切线DE,
∴∠ABE=90°,

∴∠BAE+∠E=90°,
∵∠DAE=90°,
∴∠BAD+∠BAE=90°,
∴∠BAD=∠E.
看了 (1)如图1,在平行四边形A...的网友还看了以下:
计算:(a+b-c)的平方乘(c-a-b)的立方+(c-a-b)(a+b-c)的四次方 2020-04-06 …
已知a的四次+b的四次+c的四次+d的四次=4abcd,判定以a,b,c,d为边的四边形的形状? 2020-05-13 …
1.设a.b.c分别是三角形ABC的三条边,且a/b=a+1/a+b+c,是判断∠A,∠B的关系. 2020-05-13 …
1.(-a)*(-a)*(-a)的三次方=2.(p-q)的七次方*(q-p)的三次方=3.(-x) 2020-05-14 …
A B C C 的四字词语 2020-05-16 …
a,b,c,d,都是正数,且a的平方=2,b的三次方=3.c的四次方=4,d的五次方=5,则a,b 2020-06-12 …
a的四次方+b的四次方+c的四次方-2*a的平方*b的平方-2*b的平方*c的平方-2*c的平方* 2020-06-12 …
设a,b,c都是正数,且满足a²b²+b²c²+c²a²>1/2(a的四次方+b的四次方+c的四次 2020-06-16 …
16a的平方b的四次方-8ab的平方c+c的四次方=? 2020-06-27 …
设abc为正整数,且a的平方+b的立方=c的四次方(a不等于b不等于c不等于1),求c的最小值 2020-07-11 …