早教吧作业答案频道 -->数学-->
如图,已知△ABC,∠ACB=90°,AC<BC,点D为AB的中点,过点D作BC的垂线,垂足为点F,过点A、C、D作O交BC于点E,连接CD、DE.(1)求证:DF为O的切线;(2)若AC=3,BC=9,求DE的长.
题目详情
如图,已知△ABC,∠ACB=90°,AC<BC,点D为AB的中点,过点D作BC的垂线,垂足为点F,过点A、C、D作 O交BC于点E,连接CD、DE.
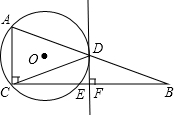
(1)求证:DF为 O的切线;
(2)若AC=3,BC=9,求DE的长.

(1)求证:DF为 O的切线;
(2)若AC=3,BC=9,求DE的长.
▼优质解答
答案和解析
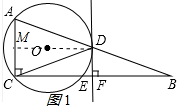 (1)证明:连接DO并延长交AC于M,如图1所示:
(1)证明:连接DO并延长交AC于M,如图1所示:
∵∠ACB=90°,AC∴CD=
AB=AD,
∴
=
,
∴DM⊥AC,
∴DM∥BC,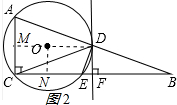
∵DF⊥BC,
∴DF⊥DO,
∴DF为 O的切线;
(2) 由(1)得:AC∥DF,
∵点D为AB的中点,
∴DF=
AC=1.5,CF=BF=
BC=4.5,
作ON⊥CE于N,连接OA,如图2所示:
则CN=EN=
CE,AM=CM=ON=DF=1.5,
设 O的半径为r,
在△AOM中,由勾股定理得:r2+(4.5-r)2=r2,
解得:r=2.5,
∴CN=EN=OM=4.5-2.5=2,
∴CE=4,
∴EF=4.5-4=0.5,
∴DE=
=
=
.
 (1)证明:连接DO并延长交AC于M,如图1所示:
(1)证明:连接DO并延长交AC于M,如图1所示:∵∠ACB=90°,AC
| 1 |
| 2 |
∴
 |
| AD |
 |
| CD |
∴DM⊥AC,
∴DM∥BC,

∵DF⊥BC,
∴DF⊥DO,
∴DF为 O的切线;
(2) 由(1)得:AC∥DF,
∵点D为AB的中点,
∴DF=
| 1 |
| 2 |
| 1 |
| 2 |
作ON⊥CE于N,连接OA,如图2所示:
则CN=EN=
| 1 |
| 2 |
设 O的半径为r,
在△AOM中,由勾股定理得:r2+(4.5-r)2=r2,
解得:r=2.5,
∴CN=EN=OM=4.5-2.5=2,
∴CE=4,
∴EF=4.5-4=0.5,
∴DE=
| EF2+DF2 |
| 0.52+1.52 |
| ||
| 2 |
看了 如图,已知△ABC,∠ACB...的网友还看了以下:
一道线性代数证明题:A为n阶实矩阵,其特征值全为实数,且AA'=A'A 证明:A=A' (A'是A 2020-04-05 …
求:A为可逆矩阵则(A*)*=|A|^(n-2)A的证明 2020-04-05 …
求解几道不等式证明1.求证:x²>4x—5.2.求证:a的四次方+1≥a的三次方+a3.已知a>0 2020-04-27 …
证集合A={x x=2n+1 n属于Z}集合B={x x=4n+-1N属于Z}证明A=B虽然我懂先 2020-05-15 …
x1+x2=b/ax1*x2=c/a的证例我已经不记得这个东西了1元2次方程希望能给一个完整的解x 2020-06-03 …
一道高中不等式的证明题a>b>0,如何证明2a+b/a+2b>a/b不总成立?(正证、反证皆可)原 2020-06-06 …
黄苔主何证:( )A.表证、寒证B.热证、里证C.里寒证D.里热证 2020-06-07 …
高数极限题1.对于数列Xn,若X2k->a(k>∞),X2k-1->a(k>∞),证明:Xn->a 2020-07-31 …
高数证明问题1.设函数f(x)在闭区间[0,A]上连续,且f(0)=0,如果f'(x)存在且为增函 2020-08-01 …
完成证明:(1)如图1,已知直线b∥c,a⊥c,求证:a⊥b证明:∵a⊥c∴∠1=∵b∥c∴∠1=∠ 2020-11-02 …