早教吧作业答案频道 -->数学-->
如图,▱ABCD的边AD与经过A、B、C三点的⊙O相切(1)求证:弧AB=弧AC(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E=1213,求tan∠D的值
题目详情
如图,▱ABCD的边AD与经过A、B、C三点的⊙O相切
(1)求证:弧AB=弧AC
(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E=
,求tan∠D的值
(1)求证:弧AB=弧AC
(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E=
| 12 |
| 13 |
▼优质解答
答案和解析
(1)证明:连接OA交BC于F.
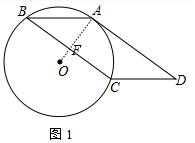
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAF=∠CFO,
∵AD是⊙O的切线,
∴∠OAD=90°,
∴∠OFC=90°,
∴OF⊥BC,
∴OA平分
,
即
=
.
(2) 如图2中,作BM⊥EC于M,AN⊥EC于N,连接AC.
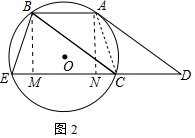
∵四边形ABCD是平行四边形,
∴∠D=∠ABC=∠BCE,
∴
=
,
∵
=
,
∴
=
=
,
∴BE=AB=AC,
=
,
∴∠E=∠ACE,
在Rt△BEM中,sin∠E=
,设BE=13m,则BM=12m,EM=5m,
在Rt△ANC中,sin∠ACN=sin∠E=
,AC=EB=13m,则CN=5m,
∵BM=CN,BM∥CN,
∴四边形BMNA是平行四边形,
∴MN=AB=EB=13m,
∴CM=18m,
∴tan∠BCE=
=
=
,
∴tan∠D=
.

∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAF=∠CFO,
∵AD是⊙O的切线,
∴∠OAD=90°,
∴∠OFC=90°,
∴OF⊥BC,
∴OA平分
 |
| BC |
即
 |
| AB |
 |
| AC |
(2) 如图2中,作BM⊥EC于M,AN⊥EC于N,连接AC.

∵四边形ABCD是平行四边形,
∴∠D=∠ABC=∠BCE,
∴
 |
| EB |
 |
| CA |
∵
 |
| BA |
 |
| AC |
∴
 |
| EB |
 |
| CA |
 |
| BA |
∴BE=AB=AC,
 |
| EA |
 |
| CB |
∴∠E=∠ACE,
在Rt△BEM中,sin∠E=
| 12 |
| 13 |
在Rt△ANC中,sin∠ACN=sin∠E=
| 12 |
| 13 |
∵BM=CN,BM∥CN,
∴四边形BMNA是平行四边形,
∴MN=AB=EB=13m,
∴CM=18m,
∴tan∠BCE=
| BM |
| CM |
| 12m |
| 18m |
| 2 |
| 3 |
∴tan∠D=
| 2 |
| 3 |
看了 如图,▱ABCD的边AD与经...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
已知集合A={y|y^2-(a^2+a+1)y+a(a^2+1)>0},B={y|}y=(1/2x 2020-06-03 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
1.已知关于x的二次三项式x的平方+mx+n有一个因式(x+5),且m+n=17,求m,n的值.2 2020-07-31 …
集合A(-1,1),集合B(b-a,a+b),a=1是A交B的充分条件,求b的范围求高手们快帮帮小 2020-08-02 …
已知抛物线C:y2=4x的焦点F,过F的直线l与C相交于A,B两点,若AB的垂直平分线l.已知抛物 2020-08-03 …
第一题:设集合M={2,-2a,a²-3},N={a²+a-4,2a+1,-1},且2∈M∩N,求实 2020-11-03 …
图中为桐乡城市abcd对应地理事物是()A.a交通通达度b土地价格c夏季平均气温d常居人口密度B.a 2020-11-25 …
递回关系式的运算公式(数列)以下是推导一个公式"a=a+r(1-p^n)/(1-p)"的过程a=p* 2021-01-13 …