早教吧作业答案频道 -->数学-->
图1和图2中,优弧AB所在O的半径为2,AB=23,点P为优弧AB上一点(点P不与A,B重合),将图形沿B
题目详情
图1和图2中,优弧
所在 O的半径为2,AB=2
,点P为优弧
上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
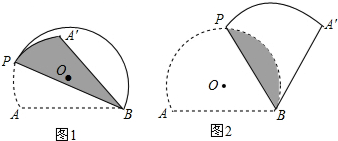
(Ⅰ)点O到弦AB的距离是___,当BP经过点O时,∠ABA′=___;
(Ⅱ)当BA′与 O相切时,如图2,求折痕的长.
 |
| AB |
| | 3 |
 |
| AB |

(Ⅰ)点O到弦AB的距离是___,当BP经过点O时,∠ABA′=___;
(Ⅱ)当BA′与 O相切时,如图2,求折痕的长.
▼优质解答
答案和解析
(1)①过点O作OH⊥AB,垂足为H,连接OB,如图1①所示.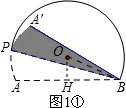
∵OH⊥AB,AB=2
,
∴AH=BH=
.
∵OB=2,
∴OH=1.
∴点O到AB的距离为1.
②当BP经过点O时,如图1②所示.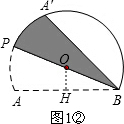
∵OH=1,OB=2,OH⊥AB,
∴sin∠OBH=
=
.
∴∠OBH=30°.
由折叠可得:∠A′BP=∠ABP=30°.
∴∠ABA′=60°.
故答案为:1、60.
(2)过点O作OG⊥BP,垂足为G,如图2所示.
∵BA′与 O相切,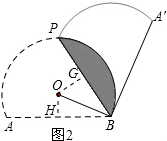
∴OB⊥A′B.
∴∠OBA′=90°.
∵∠OBH=30°,
∴∠ABA′=120°.
∴∠A′BP=∠ABP=60°.
∴∠OBP=30°.
∴OG=
OB=1.
∴BG=
.
∵OG⊥BP,
∴BG=PG=
.
∴BP=2
.
∴折痕的长为2
.

∵OH⊥AB,AB=2
| 3 |
∴AH=BH=
| 3 |
∵OB=2,
∴OH=1.
∴点O到AB的距离为1.
②当BP经过点O时,如图1②所示.

∵OH=1,OB=2,OH⊥AB,
∴sin∠OBH=
| OH |
| OB |
| 1 |
| 2 |
∴∠OBH=30°.
由折叠可得:∠A′BP=∠ABP=30°.
∴∠ABA′=60°.
故答案为:1、60.
(2)过点O作OG⊥BP,垂足为G,如图2所示.
∵BA′与 O相切,

∴OB⊥A′B.
∴∠OBA′=90°.
∵∠OBH=30°,
∴∠ABA′=120°.
∴∠A′BP=∠ABP=60°.
∴∠OBP=30°.
∴OG=
| 1 |
| 2 |
∴BG=
| 3 |
∵OG⊥BP,
∴BG=PG=
| 3 |
∴BP=2
| 3 |
∴折痕的长为2
| 3 |
看了 图1和图2中,优弧AB所在O...的网友还看了以下:
如图,已知点O为直线AB上一点,将一直角三角板的直角顶点放在点O处.(1)如图1,将三角板的一边O 2020-04-06 …
如图1,O为直线AB上的一点,过O作射线OC,将一个直角三角板的直角顶点放于O处,一边ON在射线O 2020-06-02 …
(1)如图1,将两个正方形的一个顶点重合放置,若∠AOD=40°,则∠COB=度;(2)如图2,将 2020-06-13 …
(2012•徐汇区二模)在Rt△ABC中,∠C=90°,AC=6,sinB=35,⊙B的半径长为1 2020-06-15 …
如图1,将两根笔直细木板MN、EF用图钉固定并平行摆放,将一根橡皮筋拉直后用图钉分别固定在MN、E 2020-07-30 …
综合与实践:问题情境:在综合实践课上,老师让同学们以“正方形纸片的剪拼”为主题展开教学活动,如图1 2020-08-02 …
如图,Rt△AOB的两直角边OB、OA分别位于x轴、y轴上,OA=6,OB=8.(1)如图1,将△A 2020-10-31 …
如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.(1)求证 2020-11-01 …
如图1,将长直木板B支成斜面,挡光片P固定在小车C的前端,光电门G固定在木板的侧面A处.让小车在斜面 2020-11-07 …
生物分类就是依据某一标准将生物分门别类,即把具有相同特征的生物归为一类,这是一种重要的思想方法.如图 2020-12-03 …