早教吧作业答案频道 -->数学-->
综合与实践:问题情境:在综合实践课上,老师让同学们以“正方形纸片的剪拼”为主题展开教学活动,如图1,将一张正方形纸片ABCD沿对角线BD剪开,得到△ABD和△BCD,点O是对角线BD的
题目详情
综合与实践:
问题情境:
在综合实践课上,老师让同学们以“正方形纸片的剪拼”为主题展开教学活动,如图1,将一张正方形纸片ABCD沿对角线BD剪开,得到△ABD和△BCD,点O是对角线BD的中点.
操作发现: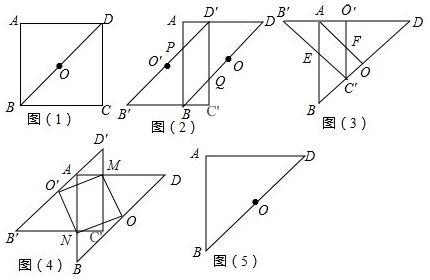
(1)将图(1)中的△BCD沿DA方向平移,点D的对应点为D′,点B的对应点为B′,点O的对应点为O′,B′D′与AB交于点P,D′C与BD交于点Q,得到图(2),则四边形D′PBQ的形状是___.
(2)“实践小组”的同学将图(1)中的△BCD以点D为旋转中心,按顺时针方向旋转45°,得到△B′C′D,点O的对应点为O′,B′C′与AB交于点E,连接AO,O′C′交于点F,得到图(3),发现四边形AEC′F是菱形,请你证明这个结论.
实践探究:
(3)“创新小组”在实践小组操作的基础上,将图(3)中的△B′C′D以点C′为旋转中心,按逆时针方向旋转,使得C′D′⊥AD,垂足为M,B′C′⊥AB,垂足为N,分别连接OM,MO′,O′N,ON,得到图(4),他们认为四边形OMO′N是正方形.“创新小组”的发现是否正确?请你说明理由.
(4)请你参照以上操作,将图(1)中的△BCD在同一平面内进行一次图形变换,得到△B′C′D′,在图(5)中画出图形变换后构造出的新图形.标明字母,说明图形变换及构图方法,写出你发现的结论,不必证明.
问题情境:
在综合实践课上,老师让同学们以“正方形纸片的剪拼”为主题展开教学活动,如图1,将一张正方形纸片ABCD沿对角线BD剪开,得到△ABD和△BCD,点O是对角线BD的中点.
操作发现:

(1)将图(1)中的△BCD沿DA方向平移,点D的对应点为D′,点B的对应点为B′,点O的对应点为O′,B′D′与AB交于点P,D′C与BD交于点Q,得到图(2),则四边形D′PBQ的形状是___.
(2)“实践小组”的同学将图(1)中的△BCD以点D为旋转中心,按顺时针方向旋转45°,得到△B′C′D,点O的对应点为O′,B′C′与AB交于点E,连接AO,O′C′交于点F,得到图(3),发现四边形AEC′F是菱形,请你证明这个结论.
实践探究:
(3)“创新小组”在实践小组操作的基础上,将图(3)中的△B′C′D以点C′为旋转中心,按逆时针方向旋转,使得C′D′⊥AD,垂足为M,B′C′⊥AB,垂足为N,分别连接OM,MO′,O′N,ON,得到图(4),他们认为四边形OMO′N是正方形.“创新小组”的发现是否正确?请你说明理由.
(4)请你参照以上操作,将图(1)中的△BCD在同一平面内进行一次图形变换,得到△B′C′D′,在图(5)中画出图形变换后构造出的新图形.标明字母,说明图形变换及构图方法,写出你发现的结论,不必证明.
▼优质解答
答案和解析
(1)∵△B'C'D'是△BCD平移得到,
∴B'D'∥BD,AD∥B'C',
∴四边形PBQD'是平行四边形,
故答案为平行四边形;
(2)∵四边形ABCD为正方形,∠ADB=∠CDB=45°,
∴将△BCD以点D为旋转中心,顺时针旋转45°后,点C′落在BD上,点B′落在DA的延长线上.
∵AB⊥AD,C′O′⊥AD,
∴AB∥O′C′.
∵B′C′⊥BD,AO⊥BD,
∴B′C′∥AO.
∴四边形AEC′F是平行四边形.
∵BD=B′D′,AD=C′D,
∴AB′=BC′,
又∵∠EAB′=∠EC′B,∠B=∠B′=45°,
∴△AB′E≌△C′BE,
∴AE=EC′,
∴四边形AEC′F菱形.
(3)“创新小组”的发现是正确的.
如图1,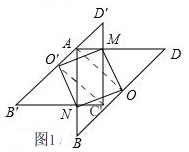 连接OA,O′C′,则四边形ANC′M是矩形.
连接OA,O′C′,则四边形ANC′M是矩形.
∵△C′MD,△AB′N是等腰直角三角形.
∴DM=MC′,AN=B′N,
又∵AB=B′C′=C′D′=AD,
∴AM=D′M=BN=NC′.
又∵OA=OD=OB,O′C′=O′D′=O′B′,
∴OA=O′C′,
∵∠OAD=∠O′D′M=∠O′C′N=∠B=45°,
∴△OAM≌△O′D′M≌△O′C′N≌△OBN,
∴OM=O′M=O′N=ON,∠MOA=∠NOB
又∵OA⊥BD,∠AOB=90°,
∴∠NOM=90°,
∴四边形NOMO′是正方形.
(4)如图2所示.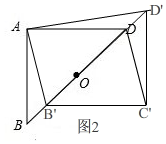
构图方法:将△BCD沿BD方向平移,得到△B′C'D′,
连接AB′、DC'.
结论:四边形AB′C'D是平行四边形.
理由:∵△B'C'D'是△BCD沿BD方向平移所得,∴AD=B'C',AD∥B'C',∴∠ADB'=∠C'B'D,
在△AB'D和△CDB'中,
,
∴△AB'D≌△CDB',
∴AD=C'B',
∵AD∥B'C',
∴四边形AB′C'D是平行四边形.
∴B'D'∥BD,AD∥B'C',
∴四边形PBQD'是平行四边形,
故答案为平行四边形;
(2)∵四边形ABCD为正方形,∠ADB=∠CDB=45°,
∴将△BCD以点D为旋转中心,顺时针旋转45°后,点C′落在BD上,点B′落在DA的延长线上.
∵AB⊥AD,C′O′⊥AD,
∴AB∥O′C′.
∵B′C′⊥BD,AO⊥BD,
∴B′C′∥AO.
∴四边形AEC′F是平行四边形.
∵BD=B′D′,AD=C′D,
∴AB′=BC′,
又∵∠EAB′=∠EC′B,∠B=∠B′=45°,
∴△AB′E≌△C′BE,
∴AE=EC′,
∴四边形AEC′F菱形.
(3)“创新小组”的发现是正确的.
如图1,
 连接OA,O′C′,则四边形ANC′M是矩形.
连接OA,O′C′,则四边形ANC′M是矩形.∵△C′MD,△AB′N是等腰直角三角形.
∴DM=MC′,AN=B′N,
又∵AB=B′C′=C′D′=AD,
∴AM=D′M=BN=NC′.
又∵OA=OD=OB,O′C′=O′D′=O′B′,
∴OA=O′C′,
∵∠OAD=∠O′D′M=∠O′C′N=∠B=45°,
∴△OAM≌△O′D′M≌△O′C′N≌△OBN,
∴OM=O′M=O′N=ON,∠MOA=∠NOB
又∵OA⊥BD,∠AOB=90°,
∴∠NOM=90°,
∴四边形NOMO′是正方形.
(4)如图2所示.

构图方法:将△BCD沿BD方向平移,得到△B′C'D′,
连接AB′、DC'.
结论:四边形AB′C'D是平行四边形.
理由:∵△B'C'D'是△BCD沿BD方向平移所得,∴AD=B'C',AD∥B'C',∴∠ADB'=∠C'B'D,
在△AB'D和△CDB'中,
|
∴△AB'D≌△CDB',
∴AD=C'B',
∵AD∥B'C',
∴四边形AB′C'D是平行四边形.
看了 综合与实践:问题情境:在综合...的网友还看了以下:
将一边长为将一边长为16厘米的正方形纸片,剪成四个大小一样的正方形,然后将其中的一个再按同样的方法 2020-05-20 …
怎么让这个的实验更好,切线方向飞出去的更明显!一根细线将笔吊上,给它一个初始的推力,笔就绕着细线做 2020-05-22 …
1.如果矩形的一条对角线长为8cm,两条对角线的一个交角为120度,求矩形的边长(精确到0.01c 2020-06-06 …
(2t11•高县)有一根如图一样弯曲的绳子,想要在虚线之间用与虚线平行的方式剪切,把绳子分成几段, 2020-07-07 …
一个正方形纸片,用剪刀沿一条不过任何顶点的直线将其剪成两部分:拿出其中一部分,再沿一条不过任何顶点 2020-07-20 …
非牛顿指数n是怎么得出的呢?是根据实验数据得出的剪切应力-速率曲线里趋势线的斜率得出呢?还是剪切粘度 2020-11-06 …
沿直线剪三刀,将长为60厘米,宽30厘米的长方形剪成若干个小长方形,这些小长方形的周长之和最小是厘米 2020-11-07 …
有一根如图一样弯曲的绳子,想要在虚线之间用与虚线平行的方式剪切,把绳子分成几段,请回答问题:(1)下 2020-12-03 …
如图所示,质量为m的带电小球用绝缘丝线悬挂于O点,处在电场强度处处相等且沿水平方向的匀强电场中,小球 2020-12-05 …
一个正方形剪掉一个角,成为五角形,然后添加一条直线把这个五角形分成两个三角形.请问怎么样添一个正方形 2020-12-25 …