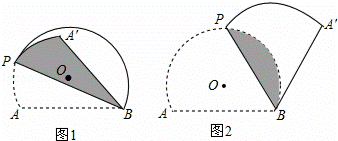
图1和图2中，优弧所在⊙O的半径为2，AB=2．点P为优弧上一点（点P不与A，B重合），将图形沿BP折叠，得到点A的对称点A′．（1）点O到弦AB

Question

图 1 和图 2 中，优弧 所在 ⊙ O 的半径为 2 ， AB=2 ．点 P 为优弧 上一点（点 P 不与 A ， B 重合），将图形沿 BP 折叠，得到点 A 的对称点 A ′ ．

（ 1 ）点 O 到弦 AB 的距离是 　 1 　 ，当 BP 经过点 O 时， ∠ ABA ′ = 　 60 　 ° ；

（ 2 ）当 BA ′ 与 ⊙ O 相切时，如图 2 ，求折痕的长：

（ 3 ）若线段 BA ′ 与优弧 只有一个公共点 B ，设 ∠ ABP= α ．确定 α 的取值范围．

Answer 1

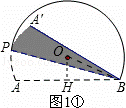
（ 1 ） ① 过点 O 作 OH ⊥ AB ，垂足为 H ，连接 OB ，如图 1 ① 所示．

∵ OH ⊥ AB ， AB=2 ，

∴ AH=BH= ．

∵ OB=2 ，

∴ OH=1 ．

∴ 点 O 到 AB 的距离为 1 ．

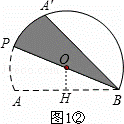
② 当 BP 经过点 O 时，如图 1 ② 所示．

∵ OH=1 ， OB=2 ， OH ⊥ AB ，

∴ sin ∠ OBH= = ．

∴∠ OBH=30 ° ．

由折叠可得： ∠ A ′ BP= ∠ ABP=30 ° ．

∴∠ ABA ′ =60 ° ．

故答案为： 1 、 60 ．

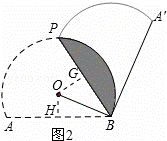
（ 2 ）过点 O 作 OG ⊥ BP ，垂足为 G ，如图 2 所示．

∵ BA ′ 与 ⊙ O 相切，

∴ OB ⊥ A ′ B ．

∴∠ OBA ′ =90 ° ．

∵∠ OBH=30 ° ，

∴∠ ABA ′ =120 ° ．

∴∠ A ′ BP= ∠ ABP=60 ° ．

∴∠ OBP=30 ° ．

∴ OG= OB=1 ．

∴ BG= ．

∵ OG ⊥ BP ，

∴ BG=PG= ．

∴ BP=2 ．

∴ 折痕的长为 2 ．

（ 3 ）若线段 BA ′ 与优弧 只有一个公共点 B ，

Ⅰ ．当点 A ′ 在 ⊙ O 的内部时，此时 α 的范围是 0 ° ＜ α ＜ 30 ° ．

Ⅱ ．当点 A ′ 在 ⊙ O 的外部时，此时 α 的范围是 60 °≤α ＜ 120 ° ．

综上所述：线段 BA ′ 与优弧 只有一个公共点 B 时， α 的取值范围是 0 ° ＜ α ＜ 30 ° 或 60 °≤α ＜ 120 ° ．