早教吧作业答案频道 -->数学-->
如图,正方形ABCD的边长为4cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.(1)求证:∠DAG=∠ABE;(2)①求证:点H总在以AB为直径的圆弧上;②画出点H所在的圆弧,并说明这
题目详情
如图,正方形ABCD的边长为4cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.
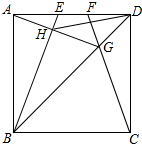
(1)求证:∠DAG=∠ABE;
(2)①求证:点H总在以AB为直径的圆弧上;
②画出点H所在的圆弧,并说明这个圆弧的两个端点字母;
(3)直接写出线段DH长度的最小值.

(1)求证:∠DAG=∠ABE;
(2)①求证:点H总在以AB为直径的圆弧上;
②画出点H所在的圆弧,并说明这个圆弧的两个端点字母;
(3)直接写出线段DH长度的最小值.
▼优质解答
答案和解析
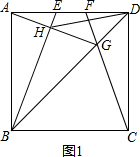 (1)证明:如图1,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
(1)证明:如图1,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠ABE=∠DCF,
在△ADG和△CDG中,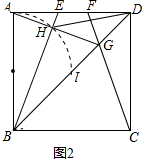
,
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCF,
∴∠DAG=∠ABE;
(2)①如图1,∵∠DAG=∠ABE,∠BAH+∠DAG=∠BAD=90°,
∴∠ABE+∠BAH=90°,
∴∠AHB=180°-90°=90°,
∴BE⊥AG,
∴点H总在以AB为直径的圆弧上;
②如图2,以AB的中点O为圆心,OA长为半径画弧,交BD于I(I是BD的中点),弧的两个端点为A和I.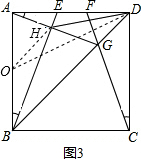
(3)如图3,取AB的中点O,连接OH、OD,
则OH=AO=
AB=2cm,
在Rt△AOD中,OD=
=
=2
,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
DH的最小值=OD-OH=2
-2.
 (1)证明:如图1,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
(1)证明:如图1,在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,在△ABE和△DCF中,
|
∴△ABE≌△DCF(SAS),
∴∠ABE=∠DCF,
在△ADG和△CDG中,

|
∴△ADG≌△CDG(SAS),
∴∠DAG=∠DCF,
∴∠DAG=∠ABE;
(2)①如图1,∵∠DAG=∠ABE,∠BAH+∠DAG=∠BAD=90°,
∴∠ABE+∠BAH=90°,
∴∠AHB=180°-90°=90°,
∴BE⊥AG,
∴点H总在以AB为直径的圆弧上;
②如图2,以AB的中点O为圆心,OA长为半径画弧,交BD于I(I是BD的中点),弧的两个端点为A和I.

(3)如图3,取AB的中点O,连接OH、OD,
则OH=AO=
| 1 |
| 2 |
在Rt△AOD中,OD=
| OA2+AD2 |
| 22+42 |
| 5 |
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
DH的最小值=OD-OH=2
| 5 |
看了 如图,正方形ABCD的边长为...的网友还看了以下:
已知,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于点 2020-05-13 …
在平行四边形ABCD中,O为对角线的交点,(见问题补充)在平行四边形ABCD中,O为对角线的交点, 2020-05-13 …
有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在正方形ABCD对角线 2020-05-16 …
将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC 2020-05-17 …
将边长为8的正方形ABCD折叠,是顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折 2020-05-17 …
过三角形一边的中点作一条第三边的平行线,与另一边的交点是否平分另一边?怎么证明? 2020-06-15 …
如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D 2020-06-27 …
如图以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交A 2020-06-27 …
证明:一个三点共线问题证明:不等边三角形的三个角的外角平分线与对边的交点是共线的三个点.(请用梅涅 2020-06-27 …
如图,在矩形ABCD中,AB=6,AD=2,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D 2020-06-30 …