圆的概念在平面内，线段PA绕它固定的一个端点P旋转一周，另一个端点A所形成的图形叫做圆，如图1所示，换言之，到某个定点等于定长的所有点在同一个圆上．拓展延伸圆心在P（a

Question

【圆的概念】在平面内，线段PA绕它固定的一个端点P旋转一周，另一个端点A所形成的图形叫做圆，如图1所示，换言之，到某个定点等于定长的所有点在同一个圆上．
【拓展延伸】圆心在P（a，b），半径为r的圆的方程可写为：（x-a）²+（y-b）²=r²．
例如：圆心在P（-1，-2），半径为5的圆的方程可写为：（x-2）²+（y+1）²=25．
（1）请填空：
①以A（3，0）为圆心，半径为1的圆的方程为：___；
②以B（-1，-2）为圆心，半径为 √(3)的圆的方程为：___；
（2）请根据以上材料解决下列问题：
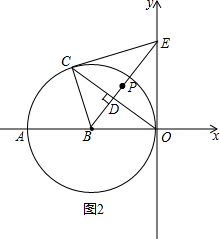
如图2所示，以B（-6，0）为圆心的圆与y轴相切于原点，C是 B上一点，连接OC，作BD⊥OC，垂足为D，延长BD交y轴于点E，已知∠AOC= (3)/(5)．
①连接EC，判断EC和 B的位置关系，并说明理由；
②在BE上是否存在一点P，使PB=PC=PE=PO？若存在，求出P点坐标，并写出以P为圆心，以PB为半径的 P的方程，若不存在，说明理由．

Answer 1

（1） ①以A（3，0）为圆心，1为半径的圆的方程为（x-3）²+y²=1；
②以B（-1，-2）为圆心，√(3)为半径的圆的方程为（x+1）²+（y+2）²=3；
故答案为（x-3）²+y²=1；（x+1）²+（y+2）²=3；

（2）①证明：∵BD⊥OC，
∴CD=OD，
∴BE垂直平分OC，
∴EO=EC，
∴∠EOC=∠ECO，
∵BO=BC，
∴∠BOC=∠BCO，
∴∠EOC+∠BOC=∠ECO+∠BCO，
∴∠BOE=∠BCE=90°，
∴BC⊥CE，
∴EC是 B的切线；
②存在．
∵∠BOE=∠BCE=90°，
∴点C和点O偶在以BE为直径的圆上，
∴当P点为BE的中点时，满足PB=PC=PE=PO，
∵B点坐标为（-6，0），
∴OB=6，
∵∠AOC+∠DOE=90°，∠DOE+∠BEO=90°，
∴∠BEO=∠AOC，
∴sin∠BEO=sin∠AOC=(3)/(5)，
在Rt△BOE中，sin∠BEO=(OB)/(BE)，
∴(6)/(BE)=(3)/(5)，
∴BE=10，
∴OE=√(BE2-OB2)=8，
∴E点坐标为（0，8），
∴线段AB的中点P的坐标为（-3，4），PB=5，
∴以P（-3，4）为圆心，以5为半径的 P的方程为（x+3）²+（y-4）²=25．