在△ABC中射影定理可表示为a=BCosC+ccoSB.其中a、b、c依次为角A、B、C的对边类比以上定理给出空间四面体性质的猜想.

Question

在△ ABC 中 射影定理可表示为 a = BC os C + c co SB .

其中 a 、 b 、 c 依次为角 A 、 B 、 C 的对边 类比以上定理 给出空间四面体性质的猜想.

Answer 1

解:如图2－1－6 在四面体 P — ABC 中 S ₁ 、 S ₂ 、 S ₃ 、 S 分别表示△ PAB 、△ PBC ₁ 、△ PCA 、△ ABC 的面积 α 、 β 、 γ 依次表示面 PAB 、面 PBC 、面 PCA 与底面 ABC 所成二面角的大小 我们猜想将射影定理类比推理到三维空间 其表现形式应为

S = S ₁ cos α + S ₂ cos β + S ₃ cos γ .

(其正确性同学们可自己证明)

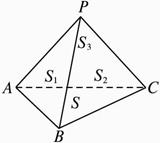
        图2－1－6

点评:运用类比推理的方法 可以帮助我们发现问题、探索规律 不少定理、公式就是运用这种方法提出 再经过严格的证明得到的.