早教吧作业答案频道 -->数学-->
如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.(1)求证:直线DM是⊙O的切线;(2)求证:DE2=DF•DA.
题目详情
如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.
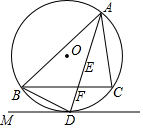
(1)求证:直线DM是⊙O的切线;
(2)求证:DE2=DF•DA.

(1)求证:直线DM是⊙O的切线;
(2)求证:DE2=DF•DA.
▼优质解答
答案和解析
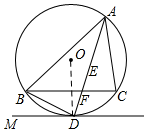 (1)如图所示,连接OD,
(1)如图所示,连接OD,
∵点E是△ABC的内心,
∴∠BAD=∠CAD,
∴
=
,
∴OD⊥BC,
又∵∠BDM=∠DAC,∠DAC=∠DBC,
∴∠BDM=∠DBC,
∴BC∥DM,
∴OD⊥DM,
∴直线DM是⊙O的切线;
(2)如图所示,连接BE,
∵点E是△ABC的内心,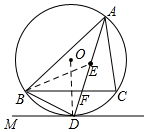
∴∠BAE=∠CAE=∠CBD,∠ABE=∠CBE,
∴∠BAE+∠ABE=∠CBD+∠CBE,
即∠BED=∠EBD,
∴DB=DE,
∵∠DBF=∠DAB,∠BDF=∠ADB,
∴△DBF∽△DAB,
∴
=
,即DB2=DF•DA,
∴DE2=DF•DA.
 (1)如图所示,连接OD,
(1)如图所示,连接OD,∵点E是△ABC的内心,
∴∠BAD=∠CAD,
∴
 |
| BD |
 |
| CD |
∴OD⊥BC,
又∵∠BDM=∠DAC,∠DAC=∠DBC,
∴∠BDM=∠DBC,
∴BC∥DM,
∴OD⊥DM,
∴直线DM是⊙O的切线;
(2)如图所示,连接BE,
∵点E是△ABC的内心,

∴∠BAE=∠CAE=∠CBD,∠ABE=∠CBE,
∴∠BAE+∠ABE=∠CBD+∠CBE,
即∠BED=∠EBD,
∴DB=DE,
∵∠DBF=∠DAB,∠BDF=∠ADB,
∴△DBF∽△DAB,
∴
| DF |
| DB |
| DB |
| DA |
∴DE2=DF•DA.
看了 如图,点E是△ABC的内心,...的网友还看了以下:
如图:正方形ABCD的边长为4cm,以AD为直径向正方形内画半圆O,E为AB上一点.请回答:点E在 2020-05-16 …
点A,O,E在同一条直线上,角AOB=40°,角COE=56°,OD平分角角COE.角DOB的度数 2020-05-17 …
如图,矩形ABCD中,AC与BD相交于点哦O,角ACB=30度,AC=16,将矩形ABCD绕点O旋 2020-06-04 …
如图,直线y=-根号3/3x+根号3分别与x轴y轴交于点A.B,⊙E经过原点O及A.B两点,⊙E经 2020-06-14 …
如图,AD是⊙O的直径,过⊙O上一点E作直线L,交AD的延长线于点B,AC⊥L于点C,AC交⊙O于 2020-06-23 …
如图,已知AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点 2020-07-24 …
如图,在Rt△ABC中,∠ABC=90°,D是AC的中点,⊙O经过A、B、D三点,CB的延长线交⊙ 2020-08-01 …
如图,在△ABC中,点O是AC边上的一个动点,过O点作直线MN‖BC,设MN交∠BCA的平分线于点 2020-08-03 …
如图,在△ABC中,AB=AC,D是BC中点,AE平分∠BAD交BC于点E,点O是AB上一点,⊙O过 2020-11-03 …
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下 2020-11-28 …