如图，已知AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D，E是AB延长线上一点，CE交⊙O于点F，连接OC、AC．（1）求证：AC平分∠DAO．（2）若∠DAO=105°，∠E=30°①求∠OCE的度数；②

Question

如图，已知AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D，E是AB延长线上一点，CE交⊙O于点F，连接OC、AC．

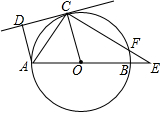
（1）求证：AC平分∠DAO．
（2）若∠DAO=105°，∠E=30°
①求∠OCE的度数；
②若⊙O的半径为2√(2)，求线段EF的长．

Answer 1

（1）∵CD是⊙O的切线，
∴OC⊥CD，
∵AD⊥CD，
∴AD∥OC，
∴∠DAC=∠OCA，
∵OC=OA，
∴∠OCA=∠OAC，
∴∠OAC=∠DAC，
∴AC平分∠DAO；

（2）①∵AD∥OC，
∴∠EOC=∠DAO=105°，
∵∠E=30°，
∴∠OCE=45°；
②作OG⊥CE于点G，

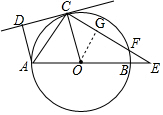
则CG=FG=OG，
∵OC=2√(2)，∠OCE=45°，
∴CG=OG=2，
∴FG=2，
在Rt△OGE中，∠E=30°，
∴GE=2√(3)，
∴EF=GE-FG=2√(3)-2．