如图，线段AB的长为302，点D在AB上，△ACD是边长为15的等边三角形，过点D作与CD垂直的射线DP，过DP上一动点G（不与D重合）作矩形CDGH，记矩形CDGH的对角线交点为O，连接OB，则线段BO的最小值

Question

如图，线段AB的长为30

√(2)，点D在AB上，△ACD是边长为15的等边三角形，过点D作与CD垂直的射线DP，过DP上一动点G（不与D重合）作矩形CDGH，记矩形CDGH的对角线交点为O，连接OB，则线段BO的最小值为（　　）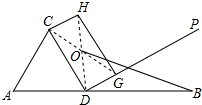

A. 15

√(2)

B. 15

C. 30

√(2)

D. 30

Answer 1

由题意可得，
当BO⊥DP时，BO取得最小值，
∵△ACD是边长为15的等边三角形，四边形CDGH是矩形，
∴∠PDB=180°-60°-90°=30°，线段AB的长为30√(2)，
∴BD=AB-AD=30√(2)-15，
∴BO的最小值是：BD•sin30°+(15)/(2)=（30√(2)-15）×(1)/(2)+(15)/(2)=15√(2)，
故选A．