已知H是锐角△ABC的垂心，以边BC的中点为圆心、过点H的圆与直线BC交于A1，A2两点，以边CA的中点为圆心、过点H的圆与直线CA交于B1、B2两点，以边AB的中点为圆心、过点H的圆与直线AB交于C1、C2

Question

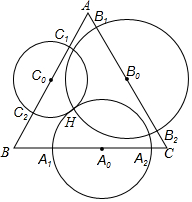
已知H是锐角△ABC的垂心，以边BC的中点为圆心、过点H的圆与直线BC交于A₁，A₂两点，以边CA的中点为圆心、过点H的圆与直线CA交于B₁、B₂两点，以边AB的中点为圆心、过点H的圆与直线AB交于C₁、C₂两点，证明：A₁，A₂，B₁，B₂，C₁，C₂六点共圆．

Answer 1

证明：如图，

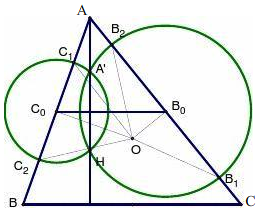
∵B₀，C₀分别是边CA，AB的中点．
设以边B₀为圆心，过点H的圆与以C₀为圆心，过点H的圆的另一个交点为A'，
则A'H⊥C₀B₀．
∵B₀，C₀分别是边CA，AB的中点，
∴C₀B₀∥BC，从而A'H⊥BC，
于是点A'在AH上．
由切割线定理：
AC₁×AC₂=AA'×AH=AB₁×AB₂，
∴B₁，B₂，C₁，C₂四点共圆．
分别作B₁B₂，C₁C₂的垂直平分线，设它们相交于点O，则O是四边形B₁B₂C₁C₂的外心，
且OB₁=OB₂=OC₁=OC₂．
同理可得，OA₁=OA₂=OB₁=OB₂，
A₁，A₂，B₁，B₂，C₁，C₂六点都是在以O为圆心，OA₁为半径的圆上，
故六点A₁，A₂，B₁，B₂，C₁，C₂共圆．