早教吧作业答案频道 -->数学-->
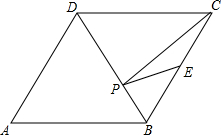
如图，菱形ABCD的边长为4cm，且∠ABC=120°，E是BC的中点，在BD上求点P，使PC+PE取最小值，并求这个最小值．
题目详情
如图，菱形ABCD的边长为4cm，且∠ABC=120°，E是BC的中点，在BD上求点P，使PC+PE取最小值，并求这个最小值．
▼优质解答
答案和解析
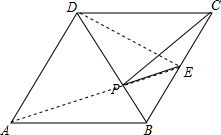如图，∵四边形ABCD是菱形，
∴点A与C关于BD对称，
连接AE交BD于P，
则AE=PC+PE取最小值，
连接DE，
∵∠ABC=120°，
∴∠DBE=60°，
∴△BCD是等边三角形，
∵E是BC的中点，
∴DE⊥BC，
∴∠BDE=30°，
∴∠ADE=90°，
∵菱形ABCD的边长为4cm，
∴AD=4，DE=2
，
∴AE=
=2
，
∴PC+PE取最小值为2
．
如图，∵四边形ABCD是菱形，∴点A与C关于BD对称，
连接AE交BD于P，
则AE=PC+PE取最小值，
连接DE，
∵∠ABC=120°，
∴∠DBE=60°，
∴△BCD是等边三角形，
∵E是BC的中点，
∴DE⊥BC，
∴∠BDE=30°，
∴∠ADE=90°，
∵菱形ABCD的边长为4cm，
∴AD=4，DE=2
| 3 |
∴AE=
| AD2+DE2 |
| 7 |
∴PC+PE取最小值为2
| 7 |
看了 如图，菱形ABCD的边长为4...的网友还看了以下：
设函数f（x）的定义域为R，若存在常数m＞0使|f（x）|≤m|x|对一切实数x均成立，则称f（x 2020-05-13 …
f(x)=x^3+ax^2-a^2x+m(a>0)若对任意的a∈[3,6],不等式f(x)≤1在X 2020-05-16 …
长100m截面积1mm的平方的铜导线（在20摄氏度时,p=0.0175欧mm的平方/m,a=0.0 2020-06-03 …
长200m,截面积1mm的平方的铜导线（在20摄氏度时,P=0.0175欧mm的平方/m,a=0. 2020-06-03 …
证明:集合A∈R,x∈A.A有界存在M∈R(M＞0),使得任意x的绝对值≦M高数证明题,这是书上的 2020-06-23 …
已知函数f(x)=Asin(2wx+π/3)+m(A>0,w>0)图像在y轴右侧的第一个最大值、最 2020-06-27 …
1.已直Lg2=a,lg3=b,试用a,b表示log512（5是底数,12是真数）2.若a+b=( 2020-07-30 …
关于充分必要条件有点糊涂,例：F(x)在X上有界的充分必要条件是它在X上既有上界又有下界.证明：首 2020-07-31 …
这步是如何得来的?已知集合A={1,3,根号M},B={1,m},A∪B=A,则m=()(A)0或根 2020-12-02 …
已知函数f（x）=ax2-（a+1）x+1，a∈R．（1）当a＞0时，求函数y=f(x)的定义域；（ 2021-01-31 …