早教吧作业答案频道 -->数学-->
如图,在四棱锥S-ABCD中,底面ABCD为菱形,E、P、Q分别是棱AD、SC、AB的中点,且SE⊥平面ABCD.(1)求证:PQ∥平面SAD;(2)求证:平面SAC⊥平面SEQ.
题目详情
如图,在四棱锥S-ABCD中,底面ABCD为菱形,E、P、Q分别是棱AD、SC、AB的中点,且SE⊥平面ABCD.
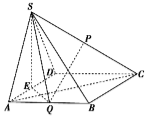
(1)求证:PQ∥平面SAD;
(2)求证:平面SAC⊥平面SEQ.

(1)求证:PQ∥平面SAD;
(2)求证:平面SAC⊥平面SEQ.
▼优质解答
答案和解析
证明: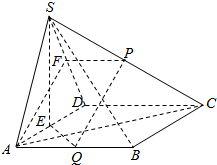 (1)取SD中点F,连结AF,PF.
(1)取SD中点F,连结AF,PF.
因为 P,F分别是棱SC,SD的中点,
所以 FP∥CD,且FP=
CD.
又因为菱形ABCD中,Q是AB的中点,
所以 AQ∥CD,且AQ=
CD.
所以 FP∥AQ且FP=AQ.
所以 AQPF为平行四边形.
所以 PQ∥AF.
又因为 PQ⊄平面SAD,
AF⊂平面SAD,
所以 PQ∥平面SAD;
(2)连结BD,
因为△SAD中SA=SD,点E棱AD的中点,
所以 SE⊥AD,
又 平面SAD⊥平面ABCD,
平面SAD∩平面ABCD=AD,
SE⊂平面SAD,
所以 SE⊥平面ABCD,
所以SE⊥AC.
因为 底面ABCD为菱形,
E,Q分别是棱AD,AB的中点,
所以 BD⊥AC,EQ∥BD.
所以 EQ⊥AC,
因为 SE∩EQ=E,
所以 AC⊥平面SEQ.
因为AC⊂平面SAC,所以平面SAC⊥平面SEQ.
 (1)取SD中点F,连结AF,PF.
(1)取SD中点F,连结AF,PF.因为 P,F分别是棱SC,SD的中点,
所以 FP∥CD,且FP=
| 1 |
| 2 |
又因为菱形ABCD中,Q是AB的中点,
所以 AQ∥CD,且AQ=
| 1 |
| 2 |
所以 FP∥AQ且FP=AQ.
所以 AQPF为平行四边形.
所以 PQ∥AF.
又因为 PQ⊄平面SAD,
AF⊂平面SAD,
所以 PQ∥平面SAD;
(2)连结BD,
因为△SAD中SA=SD,点E棱AD的中点,
所以 SE⊥AD,
又 平面SAD⊥平面ABCD,
平面SAD∩平面ABCD=AD,
SE⊂平面SAD,
所以 SE⊥平面ABCD,
所以SE⊥AC.
因为 底面ABCD为菱形,
E,Q分别是棱AD,AB的中点,
所以 BD⊥AC,EQ∥BD.
所以 EQ⊥AC,
因为 SE∩EQ=E,
所以 AC⊥平面SEQ.
因为AC⊂平面SAC,所以平面SAC⊥平面SEQ.
看了 如图,在四棱锥S-ABCD中...的网友还看了以下:
一个矩形运动场被分隔成A、B、A、B、C共5个区,A区是边长为a米的正方形,C区是边长为c米的正方 2020-06-12 …
如果一个等腰三角形的一个底角是30°,那么这个三角形按角分类是三角形.如果一个等腰三角形的一个顶角 2020-06-12 …
如图,矩形ABCD中,AB=8,BC=10,点P在矩形的边DC上由D向C运动.沿直线AP翻折△AD 2020-06-13 …
如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.(1)求证:四边形BCDE位似于四边形B 2020-06-13 …
用两个一样的直角三角形和一个等腰直角三角形(腰等于前两个直角三角形的斜边)可以拼成一个直角梯形.如 2020-06-27 …
如图,在平行四边形ABCD中,联结BD,过点C作CO⊥BD.垂足为O.并延长CO至E,使OE=CO 2020-07-21 …
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;(2)如图2,动点P、Q分别 2020-08-01 …
(1)将上面的图形A向右平移10格,得到图形B.(2)以直线L为对称轴,作图形A的轴对称图形.得到 2020-08-03 …
如图1,直线l上有三个正方形a、b、c,其中a和c称为正放置的正方形,b称为斜放置的正方形.如果a和 2020-12-30 …
(2014•海口二模)如图是一个根据△ABC的三条边的边长a,b,c判断三角形形状的程序框图,则框图 2021-01-15 …