早教吧作业答案频道 -->数学-->
如图,在平行四边形ABCD中,联结BD,过点C作CO⊥BD.垂足为O.并延长CO至E,使OE=CO.(1)联结BE、ED,如果BE⊥ED,求证:四边形ABCD是矩形;(2)联结AE、ED,求证:四边形ABDE是等腰梯形.
题目详情
如图,在平行四边形ABCD中,联结BD,过点C作CO⊥BD.垂足为O.并延长CO至E,使OE=CO.
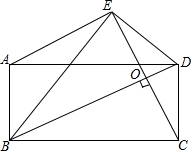
(1)联结BE、ED,如果BE⊥ED,求证:四边形ABCD是矩形;
(2)联结AE、ED,求证:四边形ABDE是等腰梯形.

(1)联结BE、ED,如果BE⊥ED,求证:四边形ABCD是矩形;
(2)联结AE、ED,求证:四边形ABDE是等腰梯形.
▼优质解答
答案和解析
(1)证明:∵CO⊥BD,OE=CO,
∴BC=BE,DC=DE,
∴∠AEC=∠ACE,∠DEC=∠DCE,
∵BE⊥ED,
∴∠BED=90°,
即∠BEO+∠DEO=90°,
∴∠BCD=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
(2)证明:∵四边形ABCD是矩形,
∴AB=DC,AD∥BC,∠BAD=90°,
∴∠ADB=∠CBD,
∵BE=BC,OC=OE,
∴∠EBD=∠CBD,
∵∠BED=∠BAD=90°,
∴A、B、D、E四点共圆,
∴∠DAE=∠DBE,
∴∠DAE=∠ADB,
∴AE∥BD,
∴四边形ABDE是梯形,
∵AB=DC,DE=DC,
∴AB=DE,
∴四边形ABDE是等腰梯形.
∴BC=BE,DC=DE,
∴∠AEC=∠ACE,∠DEC=∠DCE,
∵BE⊥ED,
∴∠BED=90°,
即∠BEO+∠DEO=90°,
∴∠BCD=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
(2)证明:∵四边形ABCD是矩形,
∴AB=DC,AD∥BC,∠BAD=90°,
∴∠ADB=∠CBD,
∵BE=BC,OC=OE,
∴∠EBD=∠CBD,
∵∠BED=∠BAD=90°,
∴A、B、D、E四点共圆,
∴∠DAE=∠DBE,
∴∠DAE=∠ADB,
∴AE∥BD,
∴四边形ABDE是梯形,
∵AB=DC,DE=DC,
∴AB=DE,
∴四边形ABDE是等腰梯形.
看了 如图,在平行四边形ABCD中...的网友还看了以下:
下图表示北半球某地二分、二至日太阳高度日变化,读图回答1-3题.1.该地的经度是( )A.15°E 2020-05-16 …
∫0−π(cosx+ex)dx=()A.1-e-πB.1+e-πC.-e-πD.πe-π-1 2020-05-17 …
设离散型随机变量X的分布律为P{X=k}=cλkk!(k=1,2,…)其中λ>0为常数,则c=() 2020-07-18 …
设函数f(x)=ex+2x-a(a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x0,y 2020-07-26 …
(2013•四川)设函数f(x)=ex+x−a(a∈R,e为自然对数的底数).若存在b∈[0,1] 2020-08-02 …
设函数f(x)=ex+2x-a(a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b)) 2020-08-02 …
已知向量a≠e,|e|=1,对任意t∈R,恒有|a-te|≥|a-e|,则[]A.a⊥eB.a⊥(a 2020-11-02 …
(2013•柳州)如图是经过轴对称变换后所得的图形,与原图形相比()A.形状没有改变,大小没有改变B 2020-11-13 …
请将下列词语的正确义项填到括号里。诘责()A.讥笑B.形容口吃C.形容人谈吐、举止文雅的样子D.这里 2020-11-27 …
(2012•江苏)A.[选修4-1:几何证明选讲]如图,AB是圆O的直径,D,E为圆上位于AB异侧的 2021-01-01 …