早教吧作业答案频道 -->数学-->
用两种方法证明“直角三角形斜边上的中线等于斜边的一半”.已知:如图1,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.求证:CD=12AB.证法1:如图2,在∠ACB的内部
题目详情
用两种方法证明“直角三角形斜边上的中线等于斜边的一半”.
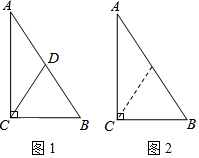
已知:如图1,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD=
AB.
证法1:如图2,在∠ACB的内部作∠BCE=∠B,
CE与AB相交于点E.
∵∠BCE=∠B,
∴___.
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵___,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE=
AB.
又∵CD是斜边AB上的中线,即CD与CE重合,
∴CD=
AB.
请把证法1补充完整,并用不同的方法完成证法2.
已知:如图1,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD=
| 1 |
| 2 |
证法1:如图2,在∠ACB的内部作∠BCE=∠B,
CE与AB相交于点E.
∵∠BCE=∠B,
∴___.
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵___,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE=
| 1 |
| 2 |
又∵CD是斜边AB上的中线,即CD与CE重合,
∴CD=
| 1 |
| 2 |
请把证法1补充完整,并用不同的方法完成证法2.

▼优质解答
答案和解析
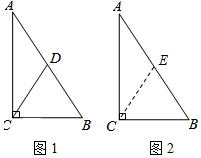 证法1:如图2,在∠ACB的内部作∠BCE=∠B,
证法1:如图2,在∠ACB的内部作∠BCE=∠B,
CE与AB相交于点E.
∵∠BCE=∠B,
∴EC=EB,
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵∠A+∠B=90°,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE=
AB.
又∵CD是斜边AB上的中线,即CD与CE重合,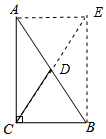
∴CD=
AB.
故答案为:EC=EB;∠A+∠B=90°;
证法2:延长CD至点E,使得DE=CD,连接AE、BE.如图3所示:
∵AD=DB,DE=CD.
∴四边形ACBE是平行四边形.
又∵∠ACB=90°,
∴四边形ACBE是矩形.
∴AB=CE,
又∵CD=
CE,
∴CD=
AB.
 证法1:如图2,在∠ACB的内部作∠BCE=∠B,
证法1:如图2,在∠ACB的内部作∠BCE=∠B,CE与AB相交于点E.
∵∠BCE=∠B,
∴EC=EB,
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵∠A+∠B=90°,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE=
| 1 |
| 2 |
又∵CD是斜边AB上的中线,即CD与CE重合,

∴CD=
| 1 |
| 2 |
故答案为:EC=EB;∠A+∠B=90°;
证法2:延长CD至点E,使得DE=CD,连接AE、BE.如图3所示:
∵AD=DB,DE=CD.
∴四边形ACBE是平行四边形.
又∵∠ACB=90°,
∴四边形ACBE是矩形.
∴AB=CE,
又∵CD=
| 1 |
| 2 |
∴CD=
| 1 |
| 2 |
看了 用两种方法证明“直角三角形斜...的网友还看了以下:
如图,△ABC中,BC=30,高AD=18,作矩形PQRS,使得P、S分别落在AB、AC边上,Q、 2020-05-13 …
如图,在梯形ABCD中AD‖BC,AB=CD=AD,BD⊥CD,D为垂足.(1)求sin∠DBC的 2020-05-15 …
如图,在等腰梯形ABCD中,AD//BC,BD平分∠ABC (1)求证:AB=AD (2)已知AD 2020-05-16 …
如图所示,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.1,求AD 2020-05-16 …
菱形ABCD的周长为40cm,它的一条对角线长10cm,1.求这个菱形的每一个内角的度数2.求菱形 2020-07-25 …
已知扇形的圆心角为120°,面积为300πcm2(1)求扇形的弧长(2)若把此扇形卷成一个圆锥,则 2020-07-26 …
如图,BC=120高AD=80,三角形ABC中内接矩形EFGH,EH:EF=2:1求矩形EFGH周 2020-08-03 …
按要求写词语1.用来形容地震景象的词语(至少2个)2.形容地震之后惨状的词语(至少2个)3.形容灾民 2020-11-27 …
急,求曲线y=x,y=1/x,x=2及x轴所围图形的面积?十分钟内急,求曲线y=x,y=1/x,x= 2020-12-19 …
梯形ABCD中,AD//BC,且AD:BC=1:3,对角线AC与BD相交于O,AE⊥BC.垂足为E, 2021-02-04 …