早教吧作业答案频道 -->数学-->
已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.(1)求证:四边形ADCE为矩形;(2)连接DE,交AC于点F,请判断四边形ABDE的形状,
题目详情
已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
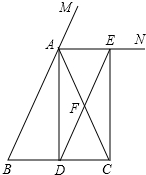
(1)求证:四边形ADCE为矩形;
(2)连接DE,交AC于点F,请判断四边形ABDE的形状,并证明;
(3)线段DF与AB有怎样的关系?请直接写出你的结论.

(1)求证:四边形ADCE为矩形;
(2)连接DE,交AC于点F,请判断四边形ABDE的形状,并证明;
(3)线段DF与AB有怎样的关系?请直接写出你的结论.
▼优质解答
答案和解析
 (1)证明:∵在△ABC中,AB=AC,AD是BC边的中线,
(1)证明:∵在△ABC中,AB=AC,AD是BC边的中线,
∴AD⊥BC,∠BAD=∠CAD,
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN,
∴∠DAE=90°,
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形;
(2)四边形ABDE是平行四边形,理由如下:
证明:由(1)知,四边形ADCE为矩形,则AE=CD,AC=DE.
又∵AB=AC,BD=CD,
∴AB=DE,AE=BD,
∴四边形ABDE是平行四边形;
(3)DF∥AB,DF=
AB.理由:
∵四边形ADCE为矩形,
∴AF=CF,
∵BD=CD,
∴DF是△ABC的中位线,
∴DF∥AB,DF=
AB.
 (1)证明:∵在△ABC中,AB=AC,AD是BC边的中线,
(1)证明:∵在△ABC中,AB=AC,AD是BC边的中线,∴AD⊥BC,∠BAD=∠CAD,
∴∠ADC=90°,
∵AN为△ABC的外角∠CAM的平分线,
∴∠MAN=∠CAN,
∴∠DAE=90°,
∵CE⊥AN,
∴∠AEC=90°,
∴四边形ADCE为矩形;
(2)四边形ABDE是平行四边形,理由如下:
证明:由(1)知,四边形ADCE为矩形,则AE=CD,AC=DE.
又∵AB=AC,BD=CD,
∴AB=DE,AE=BD,
∴四边形ABDE是平行四边形;
(3)DF∥AB,DF=
| 1 |
| 2 |
∵四边形ADCE为矩形,
∴AF=CF,
∵BD=CD,
∴DF是△ABC的中位线,
∴DF∥AB,DF=
| 1 |
| 2 |
看了 已知:如图,在△ABC中,A...的网友还看了以下:
如图1所示,已知OPQ是半径为1,圆心角为θ的扇形,A是扇形弧PQ上的动点,AB∥OQ,OP与AB 2020-05-16 …
已知直线y=1/3x+2与y轴交于点A,与x轴交于点B,直线l经过点A,坐标原点为O点,把三角形A 2020-05-16 …
如图所示,四边形ABCD是菱形,对角线AC与BD,相交与O角ACD=30度,BD=6 (1)证AB 2020-05-16 …
关于向量和三角形的题目,急几已知三角形oab,g为三角形oab的重心,pq为过g点的直线并且与oa 2020-05-16 …
下图的正方形网格,每个正方形定点交格点,每个正方形的边长为1.(1)请在图上画出线段AB=根号2( 2020-05-16 …
用若干根火柴首尾相接摆成一个矩形,设一根火柴的长度为1,矩形的两条邻边的长分别为X,Y,并要求摆成 2020-06-18 …
等边三角形ABC,AB=a,O为三角形的中心,过O点的直线交AB于M,交AC于N,求1.等边三角形 2020-08-03 …
一、已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图 2020-11-07 …
一、已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图 2020-11-07 …
如图1,已知线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2, 2020-11-07 …