早教吧作业答案频道 -->数学-->
在平面直角坐标系中,已知点A(-2,0),B(2,0),C(3,5).(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;(2)求过点A,B及抛物线的顶点D的P的圆心P的坐标;(3)在
题目详情
在平面直角坐标系中,已知点A(-2,0),B(2,0),C(3,5).
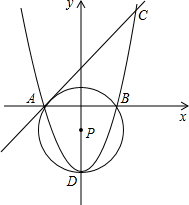
(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;
(2)求过点A,B及抛物线的顶点D的 P的圆心P的坐标;
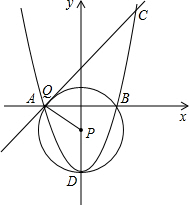
(3)在抛物线上是否存在点Q,使AQ与 P相切,若存在请求出Q点坐标.

(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;
(2)求过点A,B及抛物线的顶点D的 P的圆心P的坐标;
(3)在抛物线上是否存在点Q,使AQ与 P相切,若存在请求出Q点坐标.
▼优质解答
答案和解析
 (1)∵A(-2,0),B(2,0);
(1)∵A(-2,0),B(2,0);
∴设二次函数的解析式为y=a(x-2)(x+2)…①,
把C(3,5)代入①得a=1;
∴二次函数的解析式为:y=x2-4;
设一次函数的解析式为:y=kx+b(k≠0)…②
把A(-2,0),C(3,5)代入②得
,
解得
,
∴一次函数的解析式为:y=x+2;
(2)设P点的坐标为(0,Py),
由(1)知D点的坐标为(0,-4);
∵A,B,D三点在 P上;
∴PB=PD;
∴22+Py2=(-4-Py)2,
解得:Py=-
;
∴P点的坐标为(0,-
);
(3)在抛物线上存在这样的点Q使直线AQ与 P相切.
理由如下:设Q点的坐标为(m,m2-4);
根据平面内两点间的距离公式得:AQ2=(m+2)2+(m2-4)2,PQ2=m2+(m2-4+
)2;
∵AP=
,
∴AP2=
;
∵直线AQ是 P的切线,
∴AP⊥AQ;
∴PQ2=AP2+AQ2,
即:m2+(m2-4+
)2=
+[(m+2)2+(m2-4)2]
解得:m1=
,m2=-2(与A点重合,舍去)
∴Q点的坐标为(
,
).
 (1)∵A(-2,0),B(2,0);
(1)∵A(-2,0),B(2,0);∴设二次函数的解析式为y=a(x-2)(x+2)…①,
把C(3,5)代入①得a=1;
∴二次函数的解析式为:y=x2-4;
设一次函数的解析式为:y=kx+b(k≠0)…②
把A(-2,0),C(3,5)代入②得
|
解得
|
∴一次函数的解析式为:y=x+2;
(2)设P点的坐标为(0,Py),
由(1)知D点的坐标为(0,-4);
∵A,B,D三点在 P上;
∴PB=PD;
∴22+Py2=(-4-Py)2,
解得:Py=-
| 3 |
| 2 |
∴P点的坐标为(0,-
| 3 |
| 2 |
(3)在抛物线上存在这样的点Q使直线AQ与 P相切.
理由如下:设Q点的坐标为(m,m2-4);
根据平面内两点间的距离公式得:AQ2=(m+2)2+(m2-4)2,PQ2=m2+(m2-4+
| 3 |
| 2 |
∵AP=
| 5 |
| 2 |
∴AP2=
| 25 |
| 4 |
∵直线AQ是 P的切线,
∴AP⊥AQ;
∴PQ2=AP2+AQ2,
即:m2+(m2-4+
| 3 |
| 2 |
| 25 |
| 4 |
解得:m1=
| 10 |
| 3 |
∴Q点的坐标为(
| 10 |
| 3 |
| 64 |
| 9 |
看了 在平面直角坐标系中,已知点A...的网友还看了以下:
已知直线l:2x-3y+1=0,点A(1,2),求:1.点A关于l的对称点A'的坐标;2.直线l关 2020-04-06 …
平面直角坐标系中,直线y=x+3x轴于A,交y轴于B,在x轴正半轴取一点C,使△ABC的面积为6. 2020-05-16 …
已知三角形三点坐标求各心的公式已知三角形各顶点坐标(X1,Y1),(X2,Y2),(X3,Y3), 2020-05-16 …
C++怎么求圆弧上的坐标C++里,已知圆中心点(x0,y0),半径r,在圆的水平方向x坐标,求垂直 2020-06-14 …
1.已知直线经过点(2.3)且在X轴、Y轴上的载距相同,求该直线的方程2.求斜率为3/4且与坐标轴 2020-06-14 …
极坐标系的问题ρ=1到底是怎样的曲线?下面是几道题1ρ=1与ρ=2cos(θ+π/3),它们相交于 2020-06-20 …
关与全站仪自建坐标我用直全站仪建立自己的坐标时,我选用简单的直角坐标系,那么在向全站仪输入坐标时关 2020-07-19 …
从P(-2,1)向直线y=1/2x-3引垂线求垂直的直线的方程和垂足坐标从P(-2,1)向直线y= 2020-07-29 …
在直角坐标系中,直线Y=KX与双曲线在直角坐标系中,直线Y=KX与双曲线Y=K除以X在第一象限的交点 2020-12-31 …
如图,在平面直角坐标系中,直线AB分别与x轴正半轴、y轴正半轴交于点A、B,OA=3,OB=根号3, 2021-02-04 …