早教吧作业答案频道 -->数学-->
已知,在△ABC中,CA=CB=10cm,O为AB的中点,E、F分别在直线AC、BC上,且∠EOF=2∠A.(1)若∠A=45°.①如图(1),连接OC,当E、F分别在线段AC、BC上时,求证:△COE≌△BOF;②如图(2),当E、
题目详情
已知,在△ABC中,CA=CB=10cm,O为AB的中点,E、F分别在直线AC、BC上,且∠EOF=2∠A.
(1)若∠A=45°.
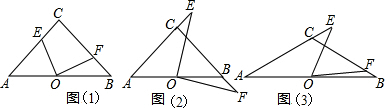
①如图(1),连接OC,当E、F分别在线段AC、BC上时,求证:△COE≌△BOF;
②如图(2),当E、F分别在AC延长线上和CB延长线上时,求CF-CE的值;
(2)如图(3),若∠A=30°,且E、F分别在AC延长线上和线段BC上,试说明CF与CE满足怎样的关系式.(提示:在直角三角形中,30°角所对的直角边等于斜边的一半)
(1)若∠A=45°.
①如图(1),连接OC,当E、F分别在线段AC、BC上时,求证:△COE≌△BOF;
②如图(2),当E、F分别在AC延长线上和CB延长线上时,求CF-CE的值;
(2)如图(3),若∠A=30°,且E、F分别在AC延长线上和线段BC上,试说明CF与CE满足怎样的关系式.(提示:在直角三角形中,30°角所对的直角边等于斜边的一半)

▼优质解答
答案和解析
(1)证明: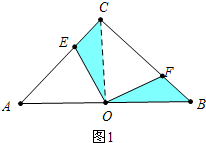 连接CO.
连接CO.
∵CA=CB,∠A=45°
∴∠A=∠B=45°,∠ACB=90°,
∵AO=OB,
∴OC=OA=OB,∠ACO=∠BCO=45°,CO⊥AB,
∵∠EOF=2∠A=90°,∠COB=90°,
∴∠EOF=∠COB,
∴∠EOC=∠BOF,
在△EOC和△FOB中,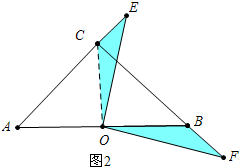
,
∴△EOC≌△FOB.
(2)如图2中,连接CO,∵∠ACO=∠ABC=45°,
∴∠ECO=∠OBF=135°,
∵∠COB=∠EOF=90°,
∴∠COE=∠BOF,
在△EOC和△FOB中
,
∴△EOC≌△FOB.
∴EC=BF,
∴CF-EC=BC+BF-EC=BC=10cm.
(3)在CF上截取CM=CO,连接OM.
∵CA=CB,∠A=30°,
∴∠A=∠B=30°,∠ACB=120°,
∵AO=OB,
∴∠ACO=∠BCO=60°
∴∠ECB=180°-∠ACB=60°,
∵∠EOF=2∠A=60°,
∴∠ECF=∠EOF,
∴E、C、O、F四点共圆,
∴∠OEF=∠OCB=60°,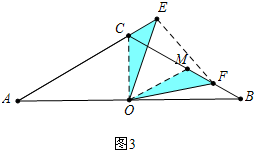
∴△OEF是等边三角形,
∴OE=OF,
∵OC=CM,∠OCM=60°,
∴△COM是等边三角形,
∴∠COM=60°=∠EOF,OC=OM=CM,
∴∠COE=∠MOF,
在△COE和△MOF中,
,
∴△COE≌△MOF,
∴CE=MF,
∴CF-CE=CM+MF-CE=CM=CO,
在RT△ACO中.∵AC=10,∠A=30°,
∴CO=
AC=5,
∴CF-CE=5.
 连接CO.
连接CO.∵CA=CB,∠A=45°
∴∠A=∠B=45°,∠ACB=90°,
∵AO=OB,
∴OC=OA=OB,∠ACO=∠BCO=45°,CO⊥AB,
∵∠EOF=2∠A=90°,∠COB=90°,
∴∠EOF=∠COB,
∴∠EOC=∠BOF,
在△EOC和△FOB中,

|
∴△EOC≌△FOB.
(2)如图2中,连接CO,∵∠ACO=∠ABC=45°,
∴∠ECO=∠OBF=135°,
∵∠COB=∠EOF=90°,
∴∠COE=∠BOF,
在△EOC和△FOB中
|
∴△EOC≌△FOB.
∴EC=BF,
∴CF-EC=BC+BF-EC=BC=10cm.
(3)在CF上截取CM=CO,连接OM.
∵CA=CB,∠A=30°,
∴∠A=∠B=30°,∠ACB=120°,
∵AO=OB,
∴∠ACO=∠BCO=60°
∴∠ECB=180°-∠ACB=60°,
∵∠EOF=2∠A=60°,
∴∠ECF=∠EOF,
∴E、C、O、F四点共圆,
∴∠OEF=∠OCB=60°,

∴△OEF是等边三角形,
∴OE=OF,
∵OC=CM,∠OCM=60°,
∴△COM是等边三角形,
∴∠COM=60°=∠EOF,OC=OM=CM,
∴∠COE=∠MOF,
在△COE和△MOF中,
|
∴△COE≌△MOF,
∴CE=MF,
∴CF-CE=CM+MF-CE=CM=CO,
在RT△ACO中.∵AC=10,∠A=30°,
∴CO=
| 1 |
| 2 |
∴CF-CE=5.
看了 已知,在△ABC中,CA=C...的网友还看了以下:
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
冠词“类别”的区别a/an/the+单数可数名词 这是可以互换吗?但又有什么差别?例:what"s 2020-05-13 …
两条直线L1、L2分别过点A(a,0)、B(-a,0)(a为常数,a不等于0),且分别绕A、B旋转 2020-07-13 …
一、已知数集M满足条件:若a∈M,则(1+a)/(1-a)∈M(a≠0,a≠±1)(1)若3∈M, 2020-07-30 …
在三角形ABC中,a,b,c分别为角A,B,C所对的边长,且a=3,A=派/3,点D在BC边上.(一 2020-11-02 …
已知三角形ABC中角ABC所对边分别为abc若ABC成等差数列b=2记角A=x,a+c=fx1已知三 2020-11-24 …
对下列词语意义的解释,正确的一组是A.别情(离别的情怀)分门别类(对事物的特征分类)别趣(特殊的意趣 2020-12-27 …
玉米胚乳蛋白质层颜色由位于两对同源染色体上的A、a和R、r两对基因共同作用而决定.A、a控制玉米基本 2021-01-12 …
函数f[x]=logaXa大于0,且a不等于1,在2,3上最大值为1,则a=当a大于1时,f(x)图 2021-01-15 …
已经知道在△ABC中,a,b,c分别∠A,∠B,∠C的对边,XXXX已经知道在△ABC中,a,b,c 2021-02-01 …