早教吧作业答案频道 -->数学-->
如图,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3,D、E分别是BC、AB的中点,F是CC1上一点,且CF=2C1F.(1)求证:C1E∥平面ADF;(2)若BC=2,求证:B1F⊥平面ADF.
题目详情
如图,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3,D、E分别是BC、AB的中点,F是CC1上一点,且CF=2C1F.
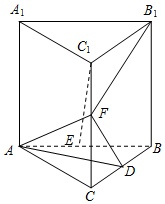
(1)求证:C1E∥平面ADF;
(2)若BC=2,求证:B1F⊥平面ADF.

(1)求证:C1E∥平面ADF;
(2)若BC=2,求证:B1F⊥平面ADF.
▼优质解答
答案和解析
证明:(1)(证法一)连接CE与AD交于点H,连接FH.
因为D是BC的中点,E是AB中点,
所以H是△ABC的重心,
所以CH=2EH,
又因为CF=2C1F,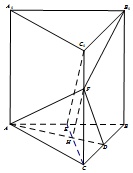
所以C1E∥FH,
因为FH⊂平面ADF,C1E⊄平面ADF,
所以C1E∥平面ADF.
(证法二)取BD中点H,连接EH,C1H.
因为H是BD的中点,E是AB中点,所以EH∥AD,
因为AD⊂平面ADF,EH⊄平面ADF,所以EH∥平面ADF,
又因为CF=2C1F,CD=2DH,所以C1H∥DF,同理C1H∥平面ADF,
∵EH∩C1H=H,所以平面C1EH∥平面ADF,
又C1E⊂平面C1EH,所以C1E∥平面ADF.
(2)因为AB=AC且D是BC中点,∴AD⊥BC,
∵直三棱柱ABC-A1B1C1,∴B1B⊥平面ABC,∴B1B⊥AD
又AD⊥BC,BB∩BC=B,∴AD⊥平面B1BCC1,∴AD⊥B1F,
∵CC1=3,CF=2C1F,∴CF=2,C1F=1,
在△B1C1F与△FCD中,∴B1C1=FC=2,C1F=CD=1,∠B1C1F=∠FCD,
∴△B1C1F≌△FCD,
∴∠C1B1F=∠CFD,∴∠C1FB1+∠CFD=90°,∴B1F⊥FD,
∵FD∩AD=D,∴B1F⊥平面ADF.
因为D是BC的中点,E是AB中点,
所以H是△ABC的重心,
所以CH=2EH,
又因为CF=2C1F,

所以C1E∥FH,
因为FH⊂平面ADF,C1E⊄平面ADF,
所以C1E∥平面ADF.
(证法二)取BD中点H,连接EH,C1H.
因为H是BD的中点,E是AB中点,所以EH∥AD,
因为AD⊂平面ADF,EH⊄平面ADF,所以EH∥平面ADF,
又因为CF=2C1F,CD=2DH,所以C1H∥DF,同理C1H∥平面ADF,
∵EH∩C1H=H,所以平面C1EH∥平面ADF,
又C1E⊂平面C1EH,所以C1E∥平面ADF.
(2)因为AB=AC且D是BC中点,∴AD⊥BC,
∵直三棱柱ABC-A1B1C1,∴B1B⊥平面ABC,∴B1B⊥AD
又AD⊥BC,BB∩BC=B,∴AD⊥平面B1BCC1,∴AD⊥B1F,
∵CC1=3,CF=2C1F,∴CF=2,C1F=1,
在△B1C1F与△FCD中,∴B1C1=FC=2,C1F=CD=1,∠B1C1F=∠FCD,
∴△B1C1F≌△FCD,
∴∠C1B1F=∠CFD,∴∠C1FB1+∠CFD=90°,∴B1F⊥FD,
∵FD∩AD=D,∴B1F⊥平面ADF.
看了 如图,在直三棱柱ABC-A1...的网友还看了以下:
求证:(1)A(n+1,n+1)-A(n,n)=n^2A(n-1,n-1);(2)C(m,n+1) 2020-06-03 …
证明不等式是什么时候要论证等号的成立比如说“若a,b,c为正实数,且a*b+b*c+c*a=0,用 2020-06-03 …
[20分][高一不等式]已知a,b,c∈R+,且a+b+c=1,求证1/a+1/b+1/c≥9已知 2020-06-10 …
a.b.c是三个不全相等的正数,且a+b+c=1,求证1-a/a+1-b/b+1-c/c>6求证( 2020-06-12 …
高二数学题,帮忙解决,要步骤的(1)设a,b,c属于R,a+b+c=0,abc0.(2)设a,b, 2020-07-22 …
证明不等式已知a,b,c是互不相等的正数,且abc=1.求证1/a+1/b+1/c>根号a+根号b 2020-08-01 …
一条关于推理与证明的问题用综合法证明:已知a,b,c已知a.b.c∈R,且a+b+c=1,求证:( 2020-08-01 …
已知a>0b>0a+b=1求证[1/a平方-1][1/b平方-1]已知a>0b>0a+b=1求证[1 2020-11-01 …
请问f(x)=a^x-b^x(a>b>1)是单增的吗?怎么证?1>a>b时呢?请问f(x)=a^x- 2020-11-03 …
高中数学不等式本人新手1,已知a≠b,求证a²+4b²>2b(a+b)2,已知a>b>0,求证1/a 2020-11-07 …