早教吧作业答案频道 -->数学-->
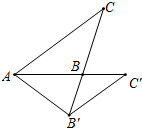
如图,△ABC中,∠ABC>90°,tan∠BAC=34,BC=4,将三角形绕着点A旋转,点C落在直线AB上的点C′处,点B落在点B′处.若C、B、B′恰好在一直线上,则AB的长为.
题目详情
如图,△ABC中,∠ABC>90°,tan∠BAC=
,BC=4,将三角形绕着点A旋转,点C落在直线AB上的点C′处,点B落在点B′处.若C、B、B′恰好在一直线上,则AB的长为___.
| 3 |
| 4 |

▼优质解答
答案和解析
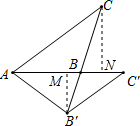 作B'M⊥AC于点M,作CN⊥AC于点N.则△BMB'∽△BNC.
作B'M⊥AC于点M,作CN⊥AC于点N.则△BMB'∽△BNC.
∵∠B'AC=∠BAC,
∴tan∠B'AC=tan∠BAC=
=
=
.
∴设B'M=3x,CN=3y,则AM=4x,AN=4y,
∴在直角△AB'M中,AB'=
=5x,
则AB=AB'=5x,
∴BM=x,
∵△BMB'∽△BNC,
∴
=
=
=3,
∴BN=
=
=y.
则5x+y=4y,
解得:x=
y.
又∵直角△BCN中,BN2+CN2=BC2
即y2+(3y)2=16,
解得:y=
,
则x=
,AB=5x=
.
故答案是:
.
 作B'M⊥AC于点M,作CN⊥AC于点N.则△BMB'∽△BNC.
作B'M⊥AC于点M,作CN⊥AC于点N.则△BMB'∽△BNC.∵∠B'AC=∠BAC,
∴tan∠B'AC=tan∠BAC=
| B′M |
| AM |
| CN |
| AN |
| 3 |
| 4 |
∴设B'M=3x,CN=3y,则AM=4x,AN=4y,
∴在直角△AB'M中,AB'=
| AM2+B′M2 |
则AB=AB'=5x,
∴BM=x,
∵△BMB'∽△BNC,
∴
| CN |
| BN |
| B′M |
| BM |
| 3x |
| x |
∴BN=
| CN |
| 3 |
| 3y |
| 3 |
则5x+y=4y,
解得:x=
| 3 |
| 5 |
又∵直角△BCN中,BN2+CN2=BC2
即y2+(3y)2=16,
解得:y=
2
| ||
| 5 |
则x=
6
| ||
| 25 |
6
| ||
| 5 |
故答案是:
6
| ||
| 5 |
看了 如图,△ABC中,∠ABC>...的网友还看了以下:
如图点F为双曲线C的左焦点,左准线l交x轴于点Q,点P是l上的一点|PQ|=|FQ|=1,且线段P 2020-04-08 …
在等腰三角形ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的的任意一点在等腰△ABC中 2020-05-20 …
在等腰三角形△ABC(C为顶点)中,CH是底边上的高线,点P是线段CH上不与端点重和的任意一点,连 2020-06-05 …
高中数学(圆锥曲线)急哟!点A(-2,0),B(2,0),动点P满足∠APB=2a,且|PA|*| 2020-06-29 …
双曲线C的一条渐近线方程是:x-2y=0,且曲线C过点(22,1).(1)求双曲线C的方程;(2) 2020-07-21 …
已知双曲线C:x的平方-y的平方=1及直线L:y=kx-1.问题1)若直线L与C的左支有两个不同的 2020-07-22 …
如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)作 2020-07-26 …
如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x0,y0)作 2020-07-26 …
已知双曲线c:x2/a2-y2/b2=1(a>0,b>0)的离心率为√2,且过点(2,√3)(1已 2020-07-30 …
下列结论中不正确的是A.直线AB和直线BA表示同一条直线B.射线AB和射线BA表示同一条射线C.线 2020-08-02 …