早教吧作业答案频道 -->数学-->
如图,长方形ABCD中,AB=4cm,BC=9cm,点E、F分别在AD、BC上,且BF=DE=3cm,连接AF、CE.(1)求证:四边形AFCE是平行四边形;(2)动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一
题目详情
如图,长方形ABCD中,AB=4cm,BC=9cm,点E、F分别在AD、BC上,且BF=DE=3cm,连接AF、CE.
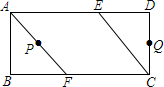
(1)求证:四边形AFCE是平行四边形;
(2)动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中:已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.

(1)求证:四边形AFCE是平行四边形;
(2)动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中:已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AD∥CB,
∵BF=DE,
∴AD-DE=CB-BF,
∴AE=FC,
∴四边形AFCE是平行四边形;
(2)当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形.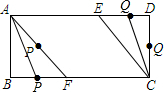
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形(如图),
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵AB=4cm,BF=3cm,
∴AF=
=5(cm),FC=9-3=6(cm),
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t-5+6,QA=13-4t,
∴5t-5+6=13-4t,解得t=
,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t=
秒.
∴AD=BC,AD∥CB,
∵BF=DE,
∴AD-DE=CB-BF,
∴AE=FC,
∴四边形AFCE是平行四边形;
(2)当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形.

因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形(如图),
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵AB=4cm,BF=3cm,
∴AF=
| 32+42 |
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t-5+6,QA=13-4t,
∴5t-5+6=13-4t,解得t=
| 4 |
| 3 |
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t=
| 4 |
| 3 |
看了 如图,长方形ABCD中,AB...的网友还看了以下:
D是线段AB的中点,C是线段AB的中垂线上一点,DE垂直AC于E,DF垂直BC于F.点C运动到什么 2020-04-27 …
在实验室中,通常将金属钠保存在()A.煤油或石蜡油中B.水中C.四氯化碳中D.汽油中 2020-05-15 …
平行四边形ABCD中,AB=8CM,AD=10CM,∠B=60°.点P从B向C运动,点Q从D向A运 2020-05-16 …
下面关于四五运动的叙述不正确的有[]A.四五运动是人民群众自发的运动B.四五运动要求审查和纠正重大 2020-07-11 …
平行四边形运动题在平行四边形ABCD中,AB=6,点P从点A出发,以1cm/秒的速度向点B运动;与 2020-07-30 …
中国共产党的创始人之一李大钊英勇就义在[]A.张作霖在北京的反革命屠杀中B.长沙反革命的“马日事变” 2020-11-05 …
“五四”运动标志着中国新民主义革命的开端,其最主要的依据是A.在“五四”运动中提出了“外争国权.内惩 2020-11-13 …
五四运动是中国新民主主义革命的开端。五四爱国运动取得初步胜利的根本原因是()A.青年学生在运动中起了 2020-11-30 …
据资料分析,地球具备生命存在的自身条件是()A.稳定的太阳光照条件B.日地距离适中C.运行的宇宙环境 2021-01-22 …
唐朝是我国诗歌的繁荣时期,诗歌风格多样,下列诗句中富有诗情画意的是[]A.海内存知己,天涯若比邻B. 2021-02-05 …