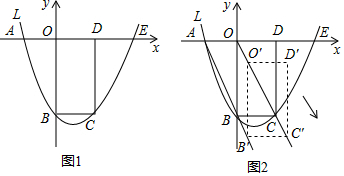
如图1，抛物线L：y=ax2+2（a-1）x-4（常数a>0）经过点A（-2，0）和点B（0，-4），与x轴的正半轴交于点E，过点B作BC⊥y轴，交L于点C，以OB，BC为边作矩形OBCD．（1）当x=2时，L取得最低点，求L的

Question

如图1，抛物线L：y=ax²+2（a-1）x-4（常数a>0）经过点A（-2，0）和点B（0，-4），与x轴的正半轴交于点E，过点B作BC⊥y轴，交L于点C，以OB，BC为边作矩形OBCD．
（1）当x=2时，L取得最低点，求L的解析式．
（2）用含a的代数式分别表示点C和点E的坐标；
（3）当S_矩形OBCD=4时，求a的值．
（4）如图2，作射线AB，OC，当AB∥OC时，将矩形OBCD从点O沿射线OC方向平移，平移后对应的矩形记作O′B′C′D′，直接写出点A到直线BD′的最大距离．

Answer 1

（1）抛物线L的对称轴是x=-(2(a-1))/(2a)，∴x=(1)/(a)-1，
∵当x=2时，L取得最低点，则(1)/(a)-1=2，
∴a=(1)/(3)，
∴L的解析式为：y=(1)/(3)x²-(4)/(3)x-4．

（2）∵在L上，且BC⊥y轴，B（0，-4），
∴设点C坐标为C（m，-4）（其中m≠0），代入L，
-4=am²+2（a-1）m-4，解得，m=(2)/(a)-2，
∴点C的坐标是（(2)/(a)-2，-4），
∵点A与点E关于L的对称轴x=(1)/(a)-1对称，A（-2，0），
设点E的坐标是（n，0）（其中n>0），
∴(1)/(a)-1-（-2）=n-（(1)/(a)-1），解得 n=(2)/(a)，
∴点E的坐标是（(2)/(a)，0）．

（3）∵S_矩形OBCD=4•|(2)/(a)-2|=4，
∴|(2)/(a)-2|=1，
当矩形OBCD在y轴右侧时，0<a<1，有(2)/(a)-2=1，解得a=(2)/(3)； 
当矩形OBCD在y轴左侧时，a>1，有(2)/(a)-2=-1，解得a=2．


（4）由图象可知，当AB⊥BD′时，点A到直线BD′的距离最大，最大距离为AB=√(OA2+OB2)=√(22+42)=2√(5)．