如图，已知关于x的二次函数y=ax2+bx+c的图象经过点（-2，y1），（-1，y2），（1，0），且y1<0<y2，对于以下结论：①abc>0；②a+3b+2c≤0；③a<-12c；④在-2<x<-1中存在一个实数x0，使得x0

Question

如图，已知关于x的二次函数y=ax²+bx+c的图象经过点（-2，y₁），（-1，y₂），（1，0），且y₁<0<y₂，对于以下结论：①abc>0；②a+3b+2c≤0；③a<-

(1)/(2)c；④在-2<x<-1中存在一个实数x₀，使得x₀=-(a+b)/(a)，其中正确的个数有（　　）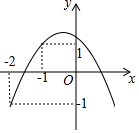

A. 1个

B. 2个

C. 3个

D. 4个

Answer 1

由题意二次函数图象如图所示，
∴a<0．b<0，c>0，
∴abc>0，故①正确．
∵-(b)/(2a)>-(1)/(2)，
∵a<0，
∴b>a，
∴b-a>0，
∵a+b+c=0，
∴c=-a-b，
∴a+3b+2c=a+3b-2a-2b=b-a>0，
∴a+3b+2c≤0，故②错误．
∵a<0，
∴b>a，
∴a-b<0，
∵a+b+c=0，
∴b=-a-c，
∴a-b=a-（-a-c）=2a+c<0，
∴a+(1)/(2)c<0，
∴a<-(1)/(2)c；故③正确；
∵y=ax²+bx+c的图象经过点（1，0），
∴a+b+c=0，
∴c=-a-b，
令y=0则ax²+bx-a-b=0，设它的两个根为x₁，1，
∵x₁•1=(-a-b)/(a)=-(a+b)/(a)，
∴x₁=-(a+b)/(a)，
∵-2<x₁<x₂，
∴在-2<x<-1中存在一个实数x₀，使得x₀=-(a+b)/(a)，故④正确，
故选D．