早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=12∠A.(1)求证:BC是O的切线;(2)若sinB=35,O的半径为r,求△EHG的面
题目详情
如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的 O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=
∠A.
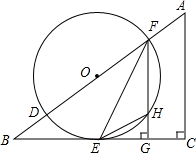
(1)求证:BC是 O的切线;
(2)若sinB=
, O的半径为r,求△EHG的面积(用含r的代数式表示).
| 1 |
| 2 |

(1)求证:BC是 O的切线;
(2)若sinB=
| 3 |
| 5 |
▼优质解答
答案和解析
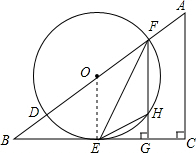 (1)证明:连接OE,
(1)证明:连接OE,
∵在△ABC中,∠C=90°,FG⊥BC,
∴∠BGF=∠C=90°,
∴FG∥AC,
∴∠OFG=∠A,
∴∠OFE=
∠OFG,
∴∠OFE=∠EFG,
∵OE=OF,
∴∠OFE=∠OEF,
∴∠OEF=∠EFG,
∴OE∥FG,
∴OE⊥BC,
∴BC是 O的切线;
(2) ∵在Rt△OBE中,sinB=
, O的半径为r,
∴OB=
r,BE=
r,
∴BF=OB+OF=
r,
∴FG=BF•sinB=
r,
∴BG=
=
r,
∴EG=BG-BE=
r,
∴S△FGE=
EG•FG=
r2,EG:FG=1:2,
∵BC是切线,
∴∠GEH=∠EFG,
∵∠EGH=∠FGE,
∴△EGH∽△FGE,
∴
=(
)=
,
∴S△EHG=
S△FGE=
r2.
 (1)证明:连接OE,
(1)证明:连接OE,∵在△ABC中,∠C=90°,FG⊥BC,
∴∠BGF=∠C=90°,
∴FG∥AC,
∴∠OFG=∠A,
∴∠OFE=
| 1 |
| 2 |
∴∠OFE=∠EFG,
∵OE=OF,
∴∠OFE=∠OEF,
∴∠OEF=∠EFG,
∴OE∥FG,
∴OE⊥BC,
∴BC是 O的切线;
(2) ∵在Rt△OBE中,sinB=
| 3 |
| 5 |
∴OB=
| 5 |
| 3 |
| 4 |
| 3 |
∴BF=OB+OF=
| 8 |
| 3 |
∴FG=BF•sinB=
| 8 |
| 5 |
∴BG=
| BF2-FG2 |
| 32 |
| 15 |
∴EG=BG-BE=
| 4 |
| 5 |
∴S△FGE=
| 1 |
| 2 |
| 16 |
| 25 |
∵BC是切线,
∴∠GEH=∠EFG,
∵∠EGH=∠FGE,
∴△EGH∽△FGE,
∴
| S△EGH |
| S△FGE |
| EG |
| FG |
| 1 |
| 4 |
∴S△EHG=
| 1 |
| 4 |
| 4 |
| 25 |
看了 如图,在△ABC中,∠C=9...的网友还看了以下:
如图是某同学设计的实验室制取二氧化碳并验证其性质的实验装置图.请回答下列问题:(1)将A、B装置连 2020-05-13 …
如图,水平地面上有两个静止的小物块a和b,其连线与墙垂直,a和b相距l,b与墙之间也相距l;a的质 2020-06-17 …
如图所示,水平地面上有两个静止的小物块a和b,其连线与墙垂直:a和b相距l;b与墙之间也相距l;a 2020-07-14 …
美国阿波罗宇宙飞船上使用了一种新型装置,其构造如图所示:(1)a、b两个电极均由多孔的碳块组成.该 2020-07-24 …
f(x)在[a,b]连续,在(a,b)二阶连续可导,证明存在c,使f(a)+f(b)-2f((a+ 2020-07-25 …
宇宙中,两颗靠得比较近的恒星,只受到彼此之间的万有引力作用互相绕转,称之为双星系统.在浩瀚的银河系中 2020-12-16 …
宇宙中两颗靠得较近的恒星只受到彼此之间的万有引力作用互相绕转,称之为双星系统.如图所示,双星A、B绕 2020-12-16 …
宇宙中,两颗靠得比较近的恒星,只受到彼此之间的万有引力作用互相绕转,称之为双星系统。在浩瀚的银河系中 2020-12-16 …
宇宙中,两颗靠得比较近的恒星,只受到彼此之间的万有引力作用相互绕转,称之为双星系统.在浩瀚的银河系中 2020-12-16 …
设f(x),g(x)在[a,b]上连续,在(a,b)内可导,且f'(x)=g'(x),x属于(a,b 2020-12-23 …