早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=23,延长AD到E,使AE=2AD,连接BE.(1)求证:△ABE为等边三角形;(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60
题目详情
如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2
,延长AD到E,使AE=2AD,连接BE.
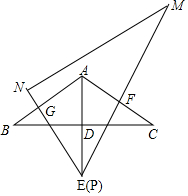
(1)求证:△ABE为等边三角形;
(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60°,边NE与AB交于点G,边ME与AC交于点F.求证:BG=AF;
(3)在(2)的条件下,求四边形AGEF的面积.
| 3 |

(1)求证:△ABE为等边三角形;
(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60°,边NE与AB交于点G,边ME与AC交于点F.求证:BG=AF;
(3)在(2)的条件下,求四边形AGEF的面积.
▼优质解答
答案和解析
(1)AB=AC,AD⊥BC,
∴∠BAE=∠CAE=
BAC=60°,∠ADB=90°,
∴∠ABD=90°-∠BAE=30°,
∴AB=2AD,
∵AE=2AD,
∴AB=AE,
∵∠BAE=60°,
∴△ABE是等边三角形.
(2)∵△ABE是等边三角形,
∴∠ABE=∠AEB=60°,
AE=BE,
由(1)∠CAE=60°
∴∠ABE=∠CAE,
∵∠NEM=∠BEA=60°,
∴∠NEM-∠AEN=∠BEA-∠AEN,
∴∠AEF=∠BEG,
在△BEG与△AEF中,
∴△BEG≌△AEF(ASA)
∴BG=AF;
(3)由(2)可知:△BEG≌△AEF,
∴S△BEG=S△AEF,
∴S四边形AGEF=S△AEG+S△AEF
=S△AEG+S△BEG
=S△ABE
∵△ABE是等边三角形,
∴AE=AB=4,
∴S△ABE=
AE•BD=
×4×2
=4
,
∴S四边形AGEF=4
∴∠BAE=∠CAE=
| 1 |
| 2 |
∴∠ABD=90°-∠BAE=30°,
∴AB=2AD,
∵AE=2AD,
∴AB=AE,
∵∠BAE=60°,
∴△ABE是等边三角形.
(2)∵△ABE是等边三角形,
∴∠ABE=∠AEB=60°,
AE=BE,
由(1)∠CAE=60°
∴∠ABE=∠CAE,
∵∠NEM=∠BEA=60°,
∴∠NEM-∠AEN=∠BEA-∠AEN,
∴∠AEF=∠BEG,
在△BEG与△AEF中,
|
∴△BEG≌△AEF(ASA)
∴BG=AF;
(3)由(2)可知:△BEG≌△AEF,
∴S△BEG=S△AEF,
∴S四边形AGEF=S△AEG+S△AEF
=S△AEG+S△BEG
=S△ABE
∵△ABE是等边三角形,
∴AE=AB=4,
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S四边形AGEF=4
| 3 |
看了 如图,在△ABC中,∠BAC...的网友还看了以下:
设平行四边形ABCD中,AC与BD交于0点,E是AD 中点,AE的延长线与CD交于点F,向量AC= 2020-05-16 …
在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE垂直BC,垂足为E,连结DE交AC于点P 2020-05-16 …
抛物线y=ax的平方+bx+c经过a[-1,0]b[3,0]c[0,3]三点其顶点为d连接bd点p 2020-05-16 …
在△ABC中,AB=AC,AC是圆0的弦.BC交圆0于D,作角ABC的外角平分线AE交圆0于E,连 2020-06-02 …
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平 2020-06-23 …
如图,AB是O的直径,D、E为O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接A 2020-07-17 …
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平 2020-08-01 …
设随机变量ξ1,ξ2,…,ξ10独立,且E(ξi)=a,D(ξi)=b,i=1,2,…,10,记η= 2020-11-02 …
(2011•德阳)如图,AB是⊙0的直径,AC切⊙0于点A,AD是⊙0的弦,OC⊥AD于F交⊙0于E 2020-11-12 …
初三几何综合在RT△ABC中,∠ACB=90°,tan∠BAC=1/2,点D在边AC上,不与A,C重 2021-02-04 …