早教吧作业答案频道 -->数学-->
已知:如图,在△ABC中,BC=BA,BE平分∠CBA交边CA于点E,∠ABC=45°,CD⊥AB,垂足为D,F为BC中点,BE与DF、DC分别交于点G、H.(1)求证:BH=CA;(2)求证:BG2=GE2+EA2.
题目详情
已知:如图,在△ABC中,BC=BA,BE平分∠CBA交边CA于点E,∠ABC=45°,CD⊥AB,垂足为D,F为BC中点,BE与DF、DC分别交于点G、H.
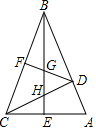
(1)求证:BH=CA;
(2)求证:BG2=GE2+EA2.

(1)求证:BH=CA;
(2)求证:BG2=GE2+EA2.
▼优质解答
答案和解析
(1)∵BC=BA,BE平分∠CBA,
∴BH⊥CA,
∴∠BEA=90°,
又CD⊥AB,∠ABC=45°,
∴∠BDC=∠CDA=90°,
∴∠BCD=∠ABC=45°,∠BAC+∠DCA=90°,∠BAC+∠ABE=90°,
∴DB=DC,∠ABE=∠DCA.
∵在△DBH与△DCA中,
∵
,
∴△DBH≌△DCA(AAS),
∴BH=AC;
(2)如图,连接CG.
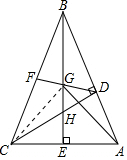
∵AB=BC,BE⊥AC,
∴BE垂直平分AC,
∴AG=CG.
又∵F点是BC的中点,DB=DC,
∴DF垂直平分BC,
∴BG=CG,
∴AG=BG,BG2=GE2+EA2.
在Rt△AGE中,∵AG2=GE2+EA2,
∴BG2=GE2+EA2.
∴BH⊥CA,
∴∠BEA=90°,
又CD⊥AB,∠ABC=45°,
∴∠BDC=∠CDA=90°,
∴∠BCD=∠ABC=45°,∠BAC+∠DCA=90°,∠BAC+∠ABE=90°,
∴DB=DC,∠ABE=∠DCA.
∵在△DBH与△DCA中,
∵
|
∴△DBH≌△DCA(AAS),
∴BH=AC;
(2)如图,连接CG.

∵AB=BC,BE⊥AC,
∴BE垂直平分AC,
∴AG=CG.
又∵F点是BC的中点,DB=DC,
∴DF垂直平分BC,
∴BG=CG,
∴AG=BG,BG2=GE2+EA2.
在Rt△AGE中,∵AG2=GE2+EA2,
∴BG2=GE2+EA2.
看了 已知:如图,在△ABC中,B...的网友还看了以下:
如图,在梯形纸片ABCD中,BC//AD,∠A+∠D=90°,tanA=2.过B点作BH⊥AD于H. 2020-03-30 …
在梯形纸片ABCD中,BC∥AD,∠A+∠D=90度,tanA=2,过点B作BH⊥AD于H,BC=B 2020-03-30 …
点E是矩形ABCD的DC边上任意一点,AE的延长线交BC的延长线于点F,直线BE交△CEF外接圆⊙ 2020-05-13 …
如图,在△ABC中,∠ABC=90°,AB=BC,过点B作BD⊥AC于D,BE平分∠DBC,交AC 2020-07-09 …
如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F, 2020-07-20 …
如图已知正方形ABCD的边长为4,E为DC上一点,且DE=3,延长AE交BC延长线于点F,连接CF 2020-07-28 …
如图,△BEF的内角∠EBF平分线BD与外角∠AEF的平分线交于点D,过D作DH∥BC分别交EF、 2020-07-29 …
(2014•绥化)如图,在矩形ABCD中,AD=2AB,∠BAD的平分线交BC于点E,DH⊥AE于 2020-07-29 …
初中平面几何,急,1.三角形ABC,角A=90度,CM垂直AB于M,AT平分角BAC交CM于D,交 2020-08-02 …
(2014•吉林)如图,四边形ABCD,AEFG都是正方形,点E,G分别在AB,AD上,连接FC,过 2020-11-12 …