早教吧作业答案频道 -->数学-->
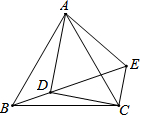
如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.(1)求证:AD=DE;(2)求∠DCE的度数;(3)若BD=1,求AD,CD的长.
题目详情
如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.

(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.
▼优质解答
答案和解析
(1)证明:∵将△ABD绕点A逆时针旋转60°得△ACE
∴△ABD≌△ACE,∠BAC=∠DAE,
∴AD=AE,BD=CE,∠AEC=∠ADB=120°,
∵△ABC为等边三角形
∴∠BAC=60°
∴∠DAE=60°
∴△ADE为等边三角形,
∴AD=DE,
(2)∠ADC=90°,∠AEC=120°,∠DAE=60°
∴∠DCE=360°-∠ADC-∠AEC-∠DAE=90°,
(3)∵△ADE为等边三角形
∴∠ADE=60°
∴∠CDE=∠ADC-∠ADE=30°
又∵∠DCE=90°
∴DE=2CE=2BD=2,
∴AD=DE=2
在Rt△DCE中,DC=
=
=
.
∴△ABD≌△ACE,∠BAC=∠DAE,
∴AD=AE,BD=CE,∠AEC=∠ADB=120°,
∵△ABC为等边三角形
∴∠BAC=60°
∴∠DAE=60°
∴△ADE为等边三角形,
∴AD=DE,
(2)∠ADC=90°,∠AEC=120°,∠DAE=60°
∴∠DCE=360°-∠ADC-∠AEC-∠DAE=90°,
(3)∵△ADE为等边三角形
∴∠ADE=60°
∴∠CDE=∠ADC-∠ADE=30°
又∵∠DCE=90°
∴DE=2CE=2BD=2,
∴AD=DE=2
在Rt△DCE中,DC=
| DE2-CE2 |
| 22-12 |
| 3 |
看了 如图,在等边△ABC中,点D...的网友还看了以下:
A、B、C、D、E、F六种元素,其中ABCDE为短周期元素,①原子半径A<C<B<E<D②原子最外 2020-05-13 …
已知集合A={正方体},B={长方体},C={正四棱柱},D={直四棱柱},E={棱柱},F={直 2020-06-27 …
Inta=3,b=5,c=7;If(a>b)a=b;c=a;If(c!=a)c=b;Printf( 2020-07-09 …
(2010•岳阳)如图为伽利略理想实验示意图,实验过程中,小球()A.在b点的速度最小B.在a点的 2020-07-15 …
在△ABC中,已知AB=AC=4cm,BC=6cm,D是BC的中点,以D为圆心作一个半径为3cm的 2020-07-26 …
如图所示,某公路(可视为x轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村 2020-11-05 …
如图,某公路(可视为x轴)的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送 2020-11-05 …
某公路的同一侧有A、B、C三个村庄,要在公路边建一货栈D,向A、B、C三个村庄送农用物资,路线是D→ 2020-11-22 …
数学题在线解答已知集合A={三角形},B={等腰三角形},C={等边三角形},D={直角三角形},那 2020-11-27 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …