早教吧作业答案频道 -->数学-->
如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.(1)求证:①AB=AD;②CD平分∠ACE.(2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加
题目详情
如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
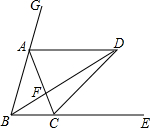
(1)求证:①AB=AD;②CD平分∠ACE.
(2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

(1)求证:①AB=AD;②CD平分∠ACE.
(2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.
▼优质解答
答案和解析
(1)①∵AD∥BE,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD;
②∵AD∥BE,
∴∠ADC=∠DCE,
由①知AB=AD,
又∵AB=AC,
∴AC=AD,
∴∠ACD=∠ADC,
∴∠ACD=∠DCE,
∴CD平分∠ACE;
(2)∠BDC=
∠BAC,
∵BD、CD分别平分∠ABE,∠ACE,
∴∠DBC=
∠ABC,∠DCE=
∠ACE,
∵∠BDC+∠DBC=∠DCE,
∴∠BDC+
∠ABC=∠ACE,
∵∠BAC+∠ABC=∠ACE,
∴∠BDC+
∠ABC=
∠ABC+
∠BAC,
∴∠BDC=
∠BAC.
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD;
②∵AD∥BE,
∴∠ADC=∠DCE,
由①知AB=AD,
又∵AB=AC,
∴AC=AD,
∴∠ACD=∠ADC,
∴∠ACD=∠DCE,
∴CD平分∠ACE;
(2)∠BDC=
| 1 |
| 2 |
∵BD、CD分别平分∠ABE,∠ACE,
∴∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BDC+∠DBC=∠DCE,
∴∠BDC+
| 1 |
| 2 |
∵∠BAC+∠ABC=∠ACE,
∴∠BDC+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BDC=
| 1 |
| 2 |
看了 如图,已知点A、C分别在∠G...的网友还看了以下:
(1).已知a,b都是正数,且a≠b,求证:2ab/a+b<(ab的开方)(2).已知a,b都是正数 2020-03-30 …
直线y=2x关于点(3,-1)对称的直线方程是___.帮我想想(a+1)/2=3,(b+2)/2= 2020-05-12 …
现在我们要来探究物体受到的滑动摩擦力大小与什么因素有关.(1)写了你的两个猜想:①②(2)现在要求 2020-05-13 …
(根号2)^2、(根号3)^2、(根号4)^2、(根号5)^2、(根号6)^2猜想a大于等于0时, 2020-05-13 …
(1)在第一个图中,求证:∠O=∠A+∠1+∠21)在第一个图中,求证:∠O=∠A+∠1+∠2(2 2020-06-26 …
在用反证法证明命题“已知a,b,c∈(0,2),求证a(2-b),b(2-c),c(2-a)不可能 2020-07-16 …
急求近世代数,素理想的证明在Z[x]中,(2,x)是极大理想,而(x)不是极大理想,但(x)是z[x 2020-11-06 …
1.已知a+a分之1=2,那么a的n次方+a的n次方分之1(n是任一自然数)等于几?.猜想并证明你的 2020-11-19 …
《三国演义》和《水浒传》的相同点是(1)作者为明末清初的小说家(2)根据民间传说改编的(3)存在许多 2020-11-23 …
1.诸子百家的思想中,值得我们利用和借鉴的是().(1)孔子的因材施教和温故而知新等教育思想(2)墨 2021-01-28 …