早教吧作业答案频道 -->数学-->
如图在△ABC中,AD⊥BC于D点,正方形EFGH的一边FG在BC上,顶点E,H分别在AB,AC上,BC=40cm,AD=30cm(1)求证:△AEH∽△ABC;(2)求正方形EFGH的边长.
题目详情
如图在△ABC中,AD⊥BC于D点,正方形EFGH的一边FG在BC上,顶点E,H分别在AB,AC上,BC=40cm,AD=30cm
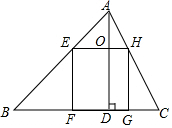
(1)求证:△AEH∽△ABC;
(2)求正方形EFGH的边长.

(1)求证:△AEH∽△ABC;
(2)求正方形EFGH的边长.
▼优质解答
答案和解析
(1)证明:∵四边形EFGH是正方形,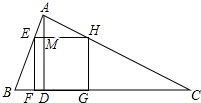
∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C,
∴△AEH∽△ABC.
(2)
∵∠EFD=∠FEO=∠FDO=90°,
∴四边形EFDO是矩形,
∴EF=DO,设正方形EFGH的边长为x,
∵△AEH∽△ABC,
∴
=
,
∴
=
,
∴x=
,
∴正方形EFGH的边长为
cm.

∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C,
∴△AEH∽△ABC.
(2)
∵∠EFD=∠FEO=∠FDO=90°,
∴四边形EFDO是矩形,
∴EF=DO,设正方形EFGH的边长为x,
∵△AEH∽△ABC,
∴
| EH |
| BC |
| AO |
| AD |
∴
| x |
| 40 |
| 30-x |
| 30 |
∴x=
| 120 |
| 7 |
∴正方形EFGH的边长为
| 120 |
| 7 |
看了 如图在△ABC中,AD⊥BC...的网友还看了以下:
变限积分求道问题对函数f(t+h)-f(t-h)在[-h,h]上的积分对h求导.F(h)=∫[-h 2020-05-23 …
设函数f,g,h∈r的r次方,且有f(x)=x+3,g(x)=2x+1,h(x)=x/2,求f°g 2020-06-12 …
已知f(X)=3X+1,g(x)=x平方,又f[h(x)+1]=g(x)求h(x) 2020-06-12 …
f(0)=0,则f(x)在x=0处可导的充要条件为A.lim(1/h^2)f(1-cosh),h→ 2020-06-12 …
f(0)=0,则f(x)在x=0处可导的充要条件为A.lim(1/h^2)f(1-cosh),h→ 2020-06-18 …
设f(x)在点a的邻域内二阶可导,求[f(a+h)+f(a-h)-2f(a)]/(h的平方)在h趋 2020-07-16 …
设函数f,g,h∈R,且有f(x)=x+3,g(x)=2x+1,h(x)=x/2,求出f○g,g○ 2020-07-26 …
求柱面的方程..准线为f(x,y)=0,z=0;母线的方向向量为s={l,m,n},则柱面的方程f 2020-07-31 …
极限换元法什么时候不能用?还是通用的?给出任意一个方程f(x),f是任意方程,可以是抽象的,h也是一 2020-12-05 …
德布罗意公式的推导问题对于一个质量为m,速度v为的电子,h为普朗克常量,p为电子动量f为频率则根据德 2020-12-28 …