如图，M为线段AB上一点，AE与BD交于点C，∠DME=∠A=∠B=α，且DM交AE于点F，ME交BD于点G．（1）写出图中的三对相似三角形；（2）连接FG，当AM=MB时，求证：△MFG∽△BMG；（3）在（2）条件下，若

Question

如图，M为线段AB上一点，AE与BD交于点C，∠DME=∠A=∠B=α，且DM交AE于点F，ME交BD于点G．

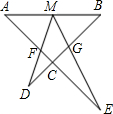
（1）写出图中的三对相似三角形；
（2）连接FG，当AM=MB时，求证：△MFG∽△BMG；
（3）在（2）条件下，若α=45°，AB=4√(2)，AF=3，求FG的长．

Answer 1

（1） △AME∽△MFE，△BMD∽△MGD，△AMF∽△BGM，
理由：∵∠AMF=∠B+∠D，∠BGM=∠DME+∠D，
又∵∠DME=∠A=∠B=α，
∴∠AMF=∠BGM，
∴△AMF∽△BGM，
∵∠D是公共角，∠DME=∠B，
∴△BMD∽△MGD，
∵∠E是公共角，∠DME=∠A，
∴△AME∽△MFE；

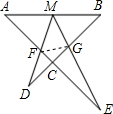（2）证明：∵△AMF∽△BGM，
∴(FM)/(GM)=(AM)/(BG)，
∵AM=BM，
∴(FM)/(GM)=(BM)/(BG)，
即(FM)/(BM)=(GM)/(BG)，
∵∠DME=∠B，
∴△MFG∽△BMG；

（3） 当α=45°时，可得AC⊥BC且AC=BC，
则AM=BM=2√(2)，
∵△AMF∽△BGM，
∴(AM)/(BG)=(AF)/(BM)，
∴BG=(AM•BM)/(AF)=(2√(2)•2√(2))/(3)=(8)/(3)，AC=BC=4√(2)•cos45°=4，
∴CG=BC-BG=4-(8)/(3)=(4)/(3)，CF=AC-AF=4-3=1，
∴FG=√(CF2+CG2)=(5)/(3)．